如本題圖①所示，四邊形ABCD內(nèi)接于⊙O，AD為直徑，過點C作CE⊥AB于點E，連接AC．
（I）求證：∠CAD=∠ECB；
（Ⅱ）如本題圖②，若CE是⊙O的切線，∠CAD=30°，連接OC．
（1）試判斷四邊形ABCO的形狀，并說明理由；
（2）當AB=2時，求AD、AC與?CD圍成的陰影部分的面積．
?
CD
【考點】圓的綜合題．
【答案】（I）見解析；（Ⅱ）（1）四邊形ABCO是菱形，理由見解析；（2）+π．
3
2
3
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/5/30 17:0:1組卷：501引用：1難度：0.3
相似題
-
1．如圖1，△ABC中，AC=5，BC=12，以AB為直徑的⊙O恰好經(jīng)過點C，延長BC至D，使得CD=BC，連結(jié)AD．
（1）求⊙O的半徑；
（2）求證：∠B=∠D；
（3）如圖2，在AD上取點P，連結(jié)PC并延長交⊙O于點Q，連結(jié)AQ交BC于點E．
①當PQ∥AB時，求AE×AQ的值；
②設AP=x,CE=y,求y關于x的函數(shù)表達式．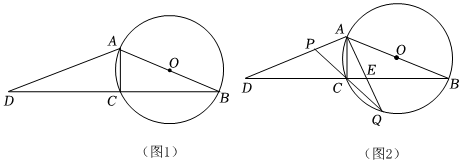
發(fā)布：2025/6/1 1:0:1組卷：726引用：4難度：0.1 -
2．如圖1，C、D是以AB為直徑的⊙O上的點，且滿足BC=CD=DA=3，點P在
上，PD交AC于點M，交AB于點G，PC交BD于點N，交AB于點H．?AB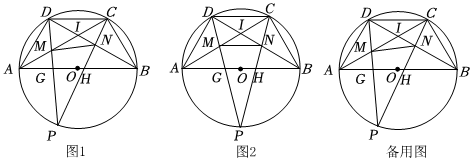
（1）求∠DBA的度數(shù)．
（2）如圖2，當點P是的中點時，?AB
①求證：△AMG是等腰三角形．
②求的值．MIAG
（3）如圖1，設，△DMI與△CNI的面積差為y,求y關于x的函數(shù)表達式．AMMC=x發(fā)布：2025/5/31 16:30:2組卷：434引用：1難度：0.2 -
3．問題發(fā)現(xiàn)：
（1）如圖1，△ABC內(nèi)接于半徑為4的⊙O，若∠C=60°，則AB=；
問題探究：
（2）如圖2，四邊形ABCD內(nèi)接于半徑為6的⊙O，若∠B=120°，求四邊形ABCD的面積最大值；
解決問題：
（3）如圖3，一塊空地由三條直路（線段AD、AB、BC）和一條弧形道路圍成，點M是AB道路上的一個地鐵站口，已知AD=BM=1千米，AM=BC=2千米，∠A=∠B=60°，?CD的半徑為1千米，市政府準備將這塊空地規(guī)劃為一個公園，主入口在點M處，另外三個入口分別在點C、D、P處，其中點P在?CD上，并在公園中修四條慢跑道，即圖中的線段DM、MC、CP、PD，是否存在一種規(guī)劃方案，使得四條慢跑道總長度（即四邊形DMCP的周長）最大？若存在，求其最大值；若不存在，說明理由．?CD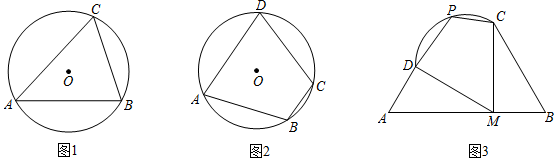
發(fā)布：2025/6/1 4:0:1組卷：929引用：5難度：0.3