（1）如圖1，已知，正方形ABCD和正方形CEFG，點G在CD邊上，點E在BC邊上，則BE與DG的數量關系為 BE=DGBE=DG；
（2）將（1）中的正方形CEFG繞點C旋轉至圖2時，（1）中的結論是否成立？若成立，請給以證明；若不成立，請說明理由；
（3）若AB=52，CE=2，將（1）中正方形CEFG繞點C旋轉α度（0＜α＜90），如圖3，當B，E，G三點在一條直線上時，求DG的長．
2
CE
=
2
【考點】四邊形綜合題．
【答案】BE=DG
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/27 11:0:2組卷：165引用：4難度：0.3
相似題
-
1．如圖①，在四邊形ABCD中，AD=BC，P是對角線BD的中點，M是DC的中點，N是AB的中點．
（1）求證：∠PMN=∠PNM．
【結論應用】
（2）如圖②，在上邊題目的條件下，延長圖中的線段AD交NM的延長線于點E，延長線段BC交NM的延長線于點F．求證：∠AEN=∠F．
（3）若（1）中的∠A+∠ABC=122°，則∠F的大小為 ．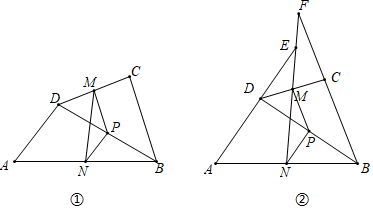
發布：2025/5/30 12:0:2組卷：194引用：7難度：0.4 -
2．小星和小紅在學習了正方形的相關知識后，對正方形內一些特殊線段的關系進行探究．
（1）問題解決
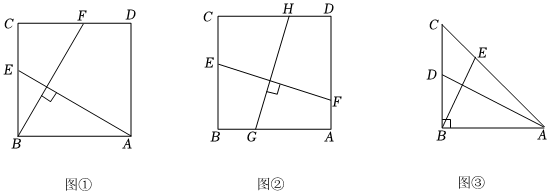
如圖①，在正方形ABCD中，E，F分別是BC，CD邊上的點，連接AE，BF，且AE⊥BF，求證：△ABE≌△BCF；
（2）類比探究
如圖②，在正方形ABCD中，E，F，G，H分別是BC，AD，AB，CD邊上的點，連接EF，GH，且EF⊥GH，求證：EF=GH；
（3）遷移應用
如圖③，在Rt△ABC中，∠ABC=90°，AB=BC，D是BC的中點，E是AC邊上的點，連接AD，BE，且BE⊥AD，求的值．AECE發布：2025/5/30 12:0:2組卷：250引用：3難度：0.1 -
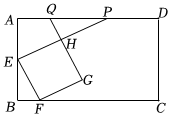3．如圖，在矩形ABCD中，點E為AB的中點，點F在BC邊上，以EF為邊，在矩形ABCD的內部作正方形EFGH，延長EH交AD邊于點P，延長GH交AD邊于點Q．
（1）若點H為EP的中點，
①求證：BE=2BF；
②若，△HQP和△AEP的周長分別為m,n,求EF=5的值；mn
（2）若S△AEP=9S△BEF，求的值．S△AEPS△HQP發布：2025/5/30 12:30:2組卷：125引用：1難度：0.3