綜合與實(shí)踐
在數(shù)學(xué)綜合實(shí)踐課上，老師讓同學(xué)們探究等腰直角三角形中的折疊問(wèn)題．
引入：
如圖，在△ABC中，AB=AC=6，∠A=90°，點(diǎn)D在邊AB上運(yùn)動(dòng)，點(diǎn)E在邊BC上運(yùn)動(dòng)．
判斷：
（1）如圖2，當(dāng)沿DE折疊，點(diǎn)B落在邊AC的點(diǎn)B′處，且DB′∥BC時(shí)，∠EB′C=9090°；四邊形BEB′D的形狀是 菱形菱形；
拓廣：
（2）如圖3，奇異小組同學(xué)的折疊方法是沿DE折疊，點(diǎn)B落在點(diǎn)B′處，延長(zhǎng)DB′交AC于點(diǎn)F，DF∥BC，點(diǎn)G在邊BC上運(yùn)動(dòng)，沿FG折疊使點(diǎn)C落在線段DB′的中點(diǎn)C′處，求線段DF的長(zhǎng)；
應(yīng)用：
（3）沿DE折疊，點(diǎn)B的對(duì)應(yīng)點(diǎn)B′恰好落在邊AC的三等分點(diǎn)處，請(qǐng)借助圖1探究，并直接寫出BD的長(zhǎng)．
【答案】90；菱形
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：296引用：3難度：0.4
相似題
-
1．已知，如圖，在△ABC中，∠ABC=90°，BD是△ABC中線，F(xiàn)是BD的中點(diǎn)，連接CF并延長(zhǎng)到E，使FE=CF，連接BE、AE．
（1）求證：△CDF≌△EBF；
（2）求證：四邊形AEBD是菱形；
（3）若BC=8，BE=5，求BG的長(zhǎng)．發(fā)布：2025/5/23 22:0:2組卷：829引用：4難度：0.5 -
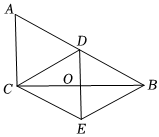2．如圖，在四邊形ABEC中，∠ACB=90°，點(diǎn)D是BA邊的中點(diǎn)，點(diǎn)E恰是點(diǎn)D關(guān)于BC所在直線的對(duì)稱點(diǎn)．
（1）證明：四邊形CEBD為菱形；
（2）連接DE交BC于點(diǎn)O，若AC=8，求線段OE的長(zhǎng)．發(fā)布：2025/5/23 23:30:1組卷：25引用：1難度：0.6 -
3．如圖，在四邊形ABCD中，AB∥CD，AD∥BC，AC平分∠DAB，連接BD交AC于點(diǎn)O，過(guò)點(diǎn)C作CE⊥AB交AB延長(zhǎng)線于點(diǎn)E．
（1）求證：四邊形ABCD為菱形；
（2）若OA=4，OB=3，求CE的長(zhǎng)．發(fā)布：2025/5/23 20:30:1組卷：3525引用：21難度：0.5