探究：
（1）【證法回顧】
證明：三角形中位線定理．
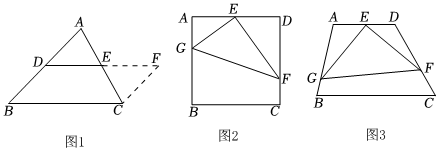
已知：如圖1，DE是△ABC的中位線．
求證：DE∥BC，DE=12BC．
證明：添加輔助線：如圖1，在△ABC中，延長DE（D、E分別是AB、AC的中點）到點F，使得EF=DE，連接CF；請繼續完成證明過程；
（2）【問題解決】
如圖2，在正方形ABCD中，E為AD的中點，G、F分別為AB、CD邊上的點，若AG=2，DF=3，∠GEF=90°，求GF的長；
（3）【拓展研究】
如圖3，在四邊形ABCD中，∠A=105°，∠D=120°，E為AD的中點，G、F分別為AB、CD邊上的點，若AG=32，DF=2，∠GEF=90°，求GF的長．
DE
=
1
2
BC
AG
=
3
2
【考點】四邊形綜合題．
【答案】（1）證明見解析過程；
（2）5；
（3）．
（2）5；
（3）
34
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：170引用：2難度：0.1
相似題
-
1．如圖1，在正方形ABCD中，點E在邊CD上（不與點C，D重合），AE交對角線BD于點G，GF⊥AE交BC于點F．
（1）求證：AG=FG．
（2）若AB=10，BF=4，求BG的長．
（3）如圖2，連接AF，EF，若AF=AE，則=．CFBF發布：2025/5/22 5:0:1組卷：475引用：1難度：0.5 -
2．在Rt△ABC中，∠C=90°，AC=8，BC=6，點D是AC邊上的動點．
（1）如圖1，過點D作DG∥AB交BC于點G，以點D為圓心，DG長為半徑畫弧，交AB于點E，在EB上截取EF=ED，連接FG．證明：四邊形DEFG是菱形；
（2）在（1）條件下，求出能作出菱形時所對應CD長度的取值范圍；
（3）如圖2，連接BD，作DQ⊥BD交AB于點Q，求AQ的最大值．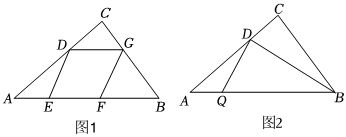
發布：2025/5/22 5:0:1組卷：143引用：2難度：0.3 -
3．問題提出：
（1）如圖1，N為正方形ABCD內一點，連接AN，DN，點M在DN延長線上，連接AM，BM，若∠BMD=∠MAN=90°，則∠AND=°；
問題解決：
（2）參觀研學觀光園是近年來興起的一種研學旅行模式．如圖2所示的五邊形AMBCD為某研學觀光園的規劃設計圖．其中AD∥BC，AD=AB=BC=400m,點P是兩條筆直的觀光小路AB與MD的交叉口，點N是小路AC與MD的交叉口，經測量∠BMD=∠MAN=∠BAD=60°．
①若點P恰為觀光小路AB的中點，求此時小路AN的長度；
②觀光園的設計者從實用和美觀的角度綜合考慮，想將園中由點B，N，C構成的三角形區域建設為采摘園，且使采摘園△BNC面積最小．是否存在這樣的面積最小的△BNC？若存在，請求出這個面積的最小值；若不存在，說明理由．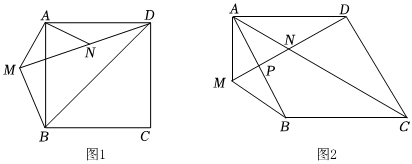
?發布：2025/5/22 5:0:1組卷：423引用：3難度：0.1