知識生成：我們已經知道，通過計算幾何圖形的面積可以表示一些代數恒等式．例如圖1可以得到（a+b）2=a2+2ab+b2，基于此，請解答下列問題：
直接應用：（1）若xy=7，x+y=5，直接寫出x2+y2的值 1111；
類比應用：（2）填空：①若x（3-x）=4，則x2+（x-3）2=11；
②若（x-2019）（x-2023）=2，則（x-2019）2+（x-2023）2=2020；
知識遷移：（3）兩塊完全相同的特制直角三角板（∠AOB=∠COD=90°）如圖2所示放置，其中A，O，D在一直線上，連接AC，BD，若AD=16，S△AOC+S△BOD=60，求一塊三角板的面積．
【答案】11；1；20
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1450引用：5難度：0.5
相似題
-
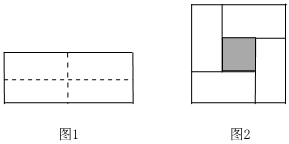1．學完整式的乘法公式后，愛思考的小麗同學為了探究公式之間的聯系，她把一個長為2a,寬為2b的長方形沿圖1中虛線用剪刀平均分成四個小長方形，然后拼成一個大正方形（如圖2）．請你根據小麗的操作回答下列問題：
（1）圖1中每個小長方形的長和寬分別為 ，圖2中大正方形的邊長為 ，中間小正方形（陰影部分）的邊長為 （均用含a,b的式子表示）；
（2）小麗發現可以用兩種方法求圖2中小正方形（陰影部分）的面積，請你幫她寫出來（直接用含a,b的式子表示，不必化簡）：方法1：，方法2：．
（3）根據（2）中的結論，探究（a+b）2，（a-b）2，ab間的等量關系．發布：2025/6/8 15:30:1組卷：50引用：1難度：0.5 -
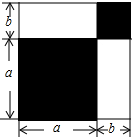2．請認真觀察圖形，解答下列問題：
（1）根據圖中條件，用兩種方法表示兩個陰影圖形的面積的和（只需表示，不必化簡）；
（2）由（1），你能得到怎樣的等量關系？請用等式表示；
（3）如果圖中的a,b（a＞b）滿足a2+b2=53，ab=14，求：
①a+b的值；
②a4-b4的值．發布：2025/6/8 16:0:1組卷：4800引用：21難度：0.3 -
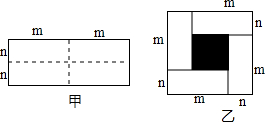3．已知圖甲是一個長為2m,寬為2n的長方形，沿圖中虛線用剪刀均剪成四個小長方形，然后拼成如圖乙所示的一個大正方形．
（1）你認為圖乙中的陰影部分的正方形的邊長=；
（2）請用兩種不同的方法求圖乙中陰影部分的面積：
方法一：
方法二：
（3）觀察圖乙，請你寫出下列代數式之間的等量關系：
（m+n）2、（m-n）2、mn
．
（4）根據（3）題中的等量關系，解決如下問題：若a+b=8，ab=7，求a-b的值．發布：2025/6/8 14:30:2組卷：702引用：3難度：0.5