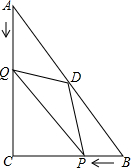
已知：如圖，在△ABC中，∠C=90°，AC=8cm,BC=6cm,D是斜邊AB的中點．點P從點B出發沿BC方向勻速運動，速度為1cm/s；同時，點Q從點A出發，沿AC方向勻速運動，速度為2cm/s.當點Q停止運動時，點P也停止運動．連接PQ、PD、QD．設運動時間為t（s）（0＜t＜4）．
（1）當t為何值時，△PQC是等腰直角三角形？
（2）設△PQD的面積為y（cm2），求y與t之間的函數關系式；是否存在某一時刻t,使△PQD的面積是Rt△ABC的面積的14？若存在，求出t的值；若不存在，請說明理由；
（3）是否存在某一時刻t,使QD⊥PD？若存在，求出t的值；若不存在，請說明理由．
1
4
【考點】相似形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：307引用：3難度：0.3
相似題
-
1．如圖，△ABC和△ADE是有公共頂點的等腰直角三角形，∠BAC=∠DAE=90°．
（1）如圖1，連結BE、CD，BE的延長線交AC于點F，交CD于點P，求證：
①△ABE≌△ACD；
②BP⊥CD；
（2）如圖2，把△ADE繞點A順時針旋轉，當點D落在AB上時，連結BE、CD，CD的延長線交BE于點P，若，BC=63，AD=3
①求證：△BDP∽△CDA；
②求△PDE的面積．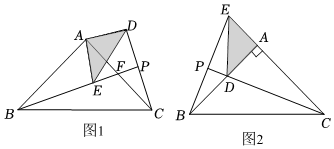
發布：2025/5/25 12:0:2組卷：294引用：3難度：0.3 -
2．【基礎鞏固】
（1）如圖1，在△ABC中，D為AB上一點，∠ACD=∠B，求證：AC2=AD?AB．
【嘗試應用】
（2）如圖2，在平行四邊形ABCD中，E為BC上一點，F為CD延長線上一點，∠BFE=∠A．若BF=5，BE=3，求AD的長．
【拓展提高】
（3）如圖3，在菱形ABCD中，E是AB上一點，F是△ABC內一點，EF∥AC，AC=2EF，∠BAD=2∠EDF，AE=1，DF=4，求菱形ABCD的邊長（直接寫出答案）．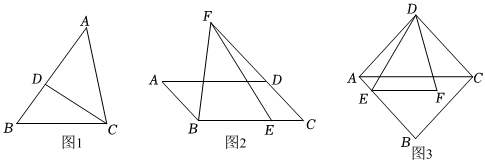
發布：2025/5/25 17:0:1組卷：480引用：4難度：0.3 -
3．問題提出
如圖（1），在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=AC，EC=DC，點E在△ABC內部，直線AD與BE交于點F．線段AF，BF，CF之間存在怎樣的數量關系？
問題探究
（1）先將問題特殊化如圖（2），當點D，F重合時，直接寫出一個等式，表示AF，BF，CF之間的數量關系；
（2）再探究一般情形如圖（1），當點D，F不重合時，證明（1）中的結論仍然成立．
問題拓展
如圖（3），在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=kAC，EC=kDC（k是常數），點E在△ABC內部，直線AD與BE交于點F．直接寫出一個等式，表示線段AF，BF，CF之間的數量關系．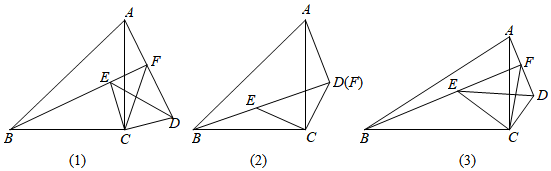
發布：2025/5/25 17:30:1組卷：5696引用：14難度：0.6