已知拋物線G：y=x2-2ax+a-1（a為常數）．
（1）當a=5時，求拋物線G的頂點坐標；
（2）若記拋物線G的頂點坐標為F（p,q），
①分別用含a的代數式表示p、q,其中p=aa，q=-a2+a-1-a2+a-1；
②請在①的基礎上繼續用含p的代數式表示q,則q=-p2+p-1-p2+p-1；
③由①②可得，頂點F的位置會隨著a取值的變化而變化，但不論a取何值，點F總落在 CC圖象上；
A．一次函數
B．正比例函數
C．二次函數
（3）小明想進一步對（2）中的問題進行如下改編：將（2）中的拋物線G改為新拋物線H；y=x2-2ax+N（a為常數），其中N為含a的代數式，使這個新拋物線H滿足新的條件：無論a取何值，它的頂點總落在某個一次函數的圖象上．
請你按照小明的改編思路，寫出一個符合以上要求的新拋物線H，使它的頂點F總是在某個一次函數的圖象上．
你寫的新拋物線H的解析式為y=x2-2ax+a2+ax2-2ax+a2+a（用含a的代數式表示），相應地，新拋物線的頂點坐標滿足的一次函數是y=kx+b（k,b為常數，k≠0），那么k=11，b=00．
【答案】a；-a2+a-1；-p2+p-1；C；x2-2ax+a2+a；1；0
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：37引用：2難度：0.5
相似題
-
1．若二次函數y=（k-1）x2+4x+1的圖象與x軸有交點，則k的取值范圍是（ ）
發布：2025/5/24 21:30:1組卷：139引用：2難度：0.7 -
2．拋物線y=ax2+bx+c（a,b,c是常數，且a＜0）經過點（3，0），對稱軸為直線x=1．下列四個結論：
①點P1（-2021，y1），P2（2022，y2）在拋物線上，則y1＜y2；
②2a+c＜0；
③關于x的方程ax2+bx+c=p的兩個實數根為x1，x2（x2＜x1），若p＞0，則x1＜3且x2＞-1；
④a（1-t2）≥b（t-1）（t為常數）．
其中正確的是 （填寫序號）．發布：2025/5/24 22:0:1組卷：188引用：1難度：0.5 -
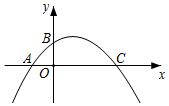3．如圖，若二次函數y=ax2+bx+c（a≠0）圖象與x軸交于點A、C與y軸交于點B，且OA=OB，則下列結論：①4ac＜b2；②bc＞0；③ac=b-1；④關于x的一元二次方程ax2+bx+c=0有一個根為；則其中結論正確的有（ ）1a發布：2025/5/24 22:30:1組卷：26引用：2難度：0.5