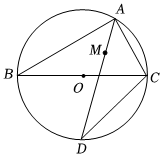
如圖，BC為△ABC外接圓⊙O的直徑，點M為△ABC的內(nèi)心，連接AM并延長交⊙O于點D，①若∠ABC=30°，⊙O的直徑為4，則扇形AOC的面積為 2π32π3；
②若∠ABC=30°，AC=2，則DMAD=3-13-1．
2
π
3
2
π
3
DM
AD
3
3
【答案】；-1
2
π
3
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/5/24 2:30:1組卷：214引用：4難度：0.5
相似題
-
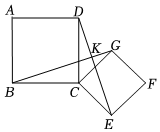1．如圖，正方形ABCD的邊長為4，正方形CEFG的邊長為，將正方形CEFG繞點C旋轉，BG和DE相交于點K，則AK的最大值是 ，連結BE，當點C正好是△BKE的內(nèi)心時，CK的長是 ．22發(fā)布：2025/5/25 16:30:1組卷：1547引用：5難度：0.1 -
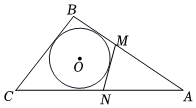2．如圖，△ABC周長為20cm,BC=6cm,圓O是△ABC的內(nèi)切圓，圓O的切線MN與AB、CA相交于點M、N，則△AMN的周長為（ ）發(fā)布：2025/5/25 9:0:1組卷：1417引用：7難度：0.5 -
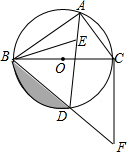3．如圖，⊙O是△ABC的外接圓，BC為⊙O的直徑，點E為△ABC的內(nèi)心，連接AE并延長交⊙O于D點，連接BD并延長至F，使得BD=DF，連接CF、BE．
（1）求證：DB=DE；
（2）求證：直線CF為⊙O的切線；
（3）若CF=4，求圖中陰影部分的面積．發(fā)布：2025/5/25 14:0:1組卷：1480引用：5難度：0.3