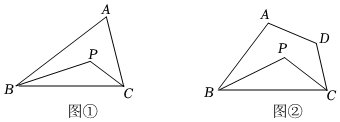
模型認識：我們學過三角形的內角和等于180°，又知道角平分線可以把一個角分成大小相等的兩部分，接下來我們就利用上述知識進行下面的探究活動．如圖①．在△ABC中，BP、CP分別是∠ABC和∠ACB的角平分線．
解決問題：
（1）若∠ABC=40°，∠ACB=80°，則∠BPC=120°120°；（直接寫出答案）
（2）若∠BAC=100°，求出∠BPC的度數：
拓展延伸：如圖②，在四邊形ABCD中，BP、CP分別是∠ABC和∠DCB的角平分線，直接寫出∠BPC與∠A+∠D的數量關系．
【答案】120°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1223引用：7難度：0.5
相似題
-
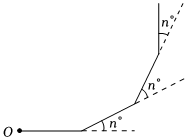1．如圖，小明從點O出發，沿直線前進5米后向左轉n°（0＜n＜90），再沿直線前進10米向左轉相同的度數，……照這樣走下去，小明發現：當他第一次回到了出發點時，共轉過了24次，則小明每次轉過的角度n的值為 ．發布：2025/6/8 10:0:2組卷：132引用：2難度：0.7 -
2．完成下面的證明：
如圖．在四邊形ABCD中，BE平分∠ABC交線段AD于點E，∠1=∠2，∠C=110°，求∠D的度數．
解：∵BE平分∠ABC（已知），
∴∠2=（ ），
又∵∠1=∠2（已知），
∴∠1=（ ），
∴AD∥BC（ ），
∴∠C+=180°（ ），
又∵∠C=110°（已知），
∴∠D=．發布：2025/6/8 11:30:1組卷：323引用：6難度：0.7 -
3．若一個正多邊形的一個內角為144°，則這個圖形為正（ ）邊形．
發布：2025/6/8 8:0:6組卷：578引用：5難度：0.8