數學活動課上,老師準備了若干張如圖1所示的三種紙片,A種紙片是邊長為a的正方形,B種紙片是邊長為b的正方形,C種紙片是長為b、寬為a的長方形.現在用A種紙片一張,B種紙片一張,C種紙片兩張拼成如圖2所示的大正方形.觀察圖形并解答下列問題.
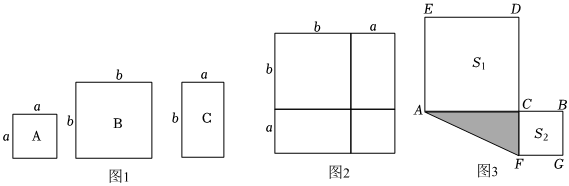
(1)由圖1到圖2的過程可得到的因式分解等式為(用含a,b的代數式表示);
(2)小敏用圖1中的A、B、C三種紙片拼出一個面積為 (3a+b)(a+2b) 的大長方形,求需要A、B、C三種紙片各多少張;
(3)如圖3,C為線段AB上的動點,分別以AC,BC為邊在AB的兩側作正方形ACDE和正方形BCFG.若AB=5,記正方形ACDE和正方形BCFG的面積分別為 S1S2,且 S1+S2=17,利用(1)中的結論求圖中三角形ACF的面積.
【答案】(1)a2+2ab+b2=(a+b)2;
(2)需要A種紙片3張,B種紙片2張,C種紙片7張;
(3)2.
(2)需要A種紙片3張,B種紙片2張,C種紙片7張;
(3)2.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/4 8:0:5組卷:322引用:1難度:0.5
相似題
-
1.我們已經學過將一個多項式分解因式的方法有提公因式法和運用公式法,其實分解因式的方法還有分組分解法、拆項法、十字相乘法等等.將一個多項式適當分組后,可提公因式或運用公式繼續分解的方法叫做分組分解.
例如:x2-2xy+y2-16=(x-y)2-16=(x-y+4)(x-y-4)
利用這種分組的思想方法解決下列問題:
(1)分解因式x2-4y2-2x+4y;
(2)△ABC三邊a,b,c滿足a2-b2-ac+bc=0判斷△ABC的形狀,并說明理由.發布:2025/6/11 9:0:1組卷:841引用:4難度:0.7 -
2.若xy=2,y-x=1,則代數式2x2y-2xy2的值為.
發布:2025/6/11 9:0:1組卷:3301引用:6難度:0.3 -
3.下列方框中的內容是小宇分解因式的解題步驟.
請回答下列問題:分解因式:(x2+4x+3)(x2+4x+5)+1.
解:設y=x2+4x.
原式=(y+3)(y+5)+1(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2+4x+4)2.(第四步)
(1)小宇分解因式中第二步到第三步運用了 .
A.提公因式法
B.平方差公式法
C.兩數和的完全平方公式法
D.兩數差的完全平方公式法
(2)小宇得到的結果能否繼續因式分解?若能,直接寫出分解因式的結果;若不能,請說明理由.
(3)請對多項式(x2+2x+6)(x2+2x-4)+25進行因式分解.發布:2025/6/11 10:30:1組卷:103引用:3難度:0.6


