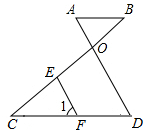
已知：如圖，AB∥CD，AD和BC交于點O，E為OC上一點，F為CD上一點，且∠CEF+∠BOD=180°．求證：∠EFC=∠A．
【考點】平行線的判定與性質．
【答案】見解析．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/7 2:0:5組卷：1061引用：17難度：0.8
相似題
-
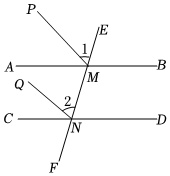1．推理填空：如圖，直線AB∥CD，并且被直線EF所截，交AB和CD于點M，N，MP平分∠AME，NQ平分∠CNE，試證明MP∥NQ．（請在橫線上填上推理內容或依據）
證明：∵AB∥CD，
∴∠AME=∠CNE（ ），
∵MP平分∠AME，NQ平分∠CNE．
∴，∠2=（ ），∠1=12∠AME
∵∠AME=∠CNE，
∴（ ），
∴MP∥NQ（ ）．發布：2025/6/7 11:30:1組卷：105引用：5難度：0.5 -
2．下面是投影屏上出示的搶答題，需要回答橫線上符號代表的內容．
已知：如圖，∠BEC=∠B+∠C，
求證：AB∥CD．
證明：過點E作EF∥AB，
則∠B=．（兩直線平行，相等）
又∠BEC=∠B+∠C（已知），∠BEC=∠BEF+∠FEC，得∠C=．（等量代換）
所以EF∥CD．（ 相等，兩直線平行）
所以AB∥CD．（平行于同一條直線的兩直線平行）
請將上述橫線處補充完整．發布：2025/6/7 12:0:1組卷：46引用：2難度：0.5 -
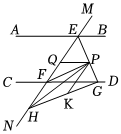3．如圖，直線MN與直線AB、CD分別交于點E、F，AB∥CD，∠BEF與∠EFD的角平分線交于點P，EP與CD交于點G，點H是MN上一點，且GH⊥EG，連接PH，K是GH上一點使∠PHK=∠HPK，作PQ平分∠EPK，交MN于點Q，∠HPQ：∠QFP=3：2，則∠EHG=．發布：2025/6/7 11:30:1組卷：759引用：3難度：0.3