利用圖形面積可以解釋代數恒等式的正確性，也可以解釋不等式的正確性．
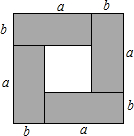
（1）根據下列所示圖形寫出一個代數恒等式；
（2）已知正數a,b,c和m,n,l,滿足a+m=b+n=c+l=k.試構造邊長為k的正方形，利用圖形面積來說明al+bm+cn＜k²．

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/5/27 15:0:2組卷：268引用：7難度：0.7

相似題

1．如圖，有兩個正方形紙板A，B，紙板A與B的面積之和為34．現將紙板B按甲方式放在紙板A的內部，陰影部分的面積為4．若將紙板A，B按乙方式并列放置后，構造新的正方形，則陰影部分的面積為（　　）
A．30 B．32 C．34 D．36
發布：2025/5/26 7:30:2組卷：414引用：8難度：0.6
解析
2．如圖，將四個小正方形用兩種不同方法放在大正方形的四個頂點，則圖2中陰影部分的面積為（　　）
A．ab B．（a+b）² C．（a-b）² D．a²-ab+b²
發布：2025/5/25 16:0:2組卷：100引用：1難度：0.7
解析
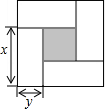3．如圖所示的是用4個全等的小長方形與1個小正方形密鋪而成的正方形圖案，已知該圖案的面積為49，小正方形的面積為4，若分別用x,y（x＞y）表示小長方形的長和寬，則下列關系式中不正確的是（　　）
A．x+y=7 B．x-y=2 C．x²+y²=25 D．4xy+4=49
發布：2025/5/26 12:0:1組卷：1034引用：8難度：0.7
解析

相關試卷

利用圖形面積可以解釋代數恒等式的正確性，也可以解釋不等式的正確性．（1）根據下列所示圖形寫出一個代數恒等式；（2）已知正數a,b,c和m,n,l,滿足a+m=b+n=c+l=k.試構造邊長為k的正方形，利用圖形面積來說明al+bm+cn＜k2．