在平面直角坐標系xOy中，拋物線y=ax2-3ax+2（a＜0）交y軸于點A，拋物線的對稱軸交x軸于點P，聯結PA．
（1）求線段PA的長；
（2）如果拋物線的頂點到直線PA的距離為3，求a的值；
（3）以點P為圓心、PA為半徑的⊙P交y軸的負半軸于點B，第一象限內的點Q在⊙P上，且劣弧?AB=2?AQ．如果拋物線經過點Q，求a的值．
?
AB
?
AQ
【考點】二次函數綜合題．
【答案】（1）PA=；
（2）a=-；
（3）a=-．
5
2
（2）a=-
4
3
（3）a=-
5
22
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：230引用：3難度：0.3
相似題
-
1．如圖1，拋物線C1：y=ax2+bx+c經過A（-1，0），B（5，0），C（0，
）三點，直線DF為該拋物線的對稱軸，連接線段AC，∠CAB的平分線AE交拋物線C1于點E．3
（1）求拋物線C1的表達式；
（2）如圖1，作點C關于x軸的對稱點C′，將原拋物線沿對稱軸向下平移經過點C′得到拋物線C2，在射線AE上取點Q，連接CQ，將射線QC繞點Q逆時針旋轉120°交拋物線C2于點P，當△CAQ為等腰三角形時，求點P的橫坐標；
（3）如圖2，將拋物線C1沿一定方向平移，使頂點D′落在射線AE上，平移后的拋物線C3與線段CB相交于點M、N，線段CB與DF相交于點Q，當點Q恰好為線段MN的中點時，求拋物線C3的頂點坐標．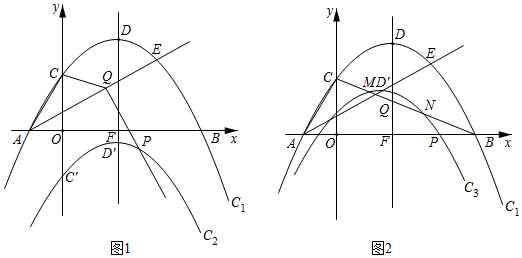
發布：2025/5/21 19:30:2組卷：1035引用：2難度：0.1 -
2．如圖①，在平面直角坐標系xOy中，直線y=
x與拋物線L1：y=ax2-2x（a＞0）在第一象限交于點A，點P為線段OA上一點（不含端點），過點P作直線l∥y軸，分別交x軸，拋物線L1于點M，Q．12
（1）若點A的橫坐標為2，求a的值；
（2）過點A作AN⊥l,垂足為N，求證：PQ=a?OM?AN；
（3）如圖②，若過點Q的拋物線L2：y=ax2-4x+b與直線y=x交于點B，C（點B在C的左側），求證：PB?PC=PO?PA．12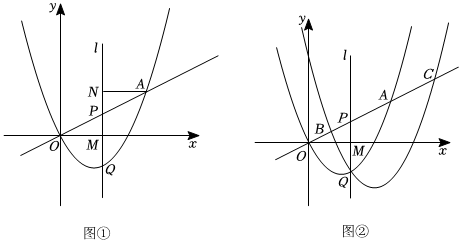
發布：2025/5/21 20:30:1組卷：372引用：1難度：0.2 -
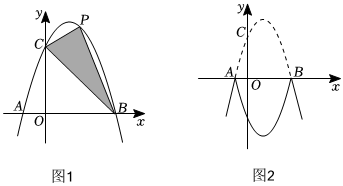
3．二次函數y=ax2+bx+3（a≠0）的圖象與x軸交于A（-1，0），B（3，0），與y軸交于點C．
（1）求該二次函數解析式；
（2）如圖1，第一象限內該二次函數圖象上有一動點P，連接BP，CP，求△BCP面積的最大值；
（3）如圖2，將該二次函數圖象在x軸上方的部分沿x軸翻折后，所得新函數圖象如圖2所示，若直線y=x+m與新函數圖象恰好有三個公共點時，則m的值為 ．發布：2025/5/21 20:30:1組卷：278引用：2難度：0.3