我們知道：x2-6x=（x2-6x+9）-9=（x-3）2-9；-x2+10=-（x2-10x+25）+25=-（x-5）2+25，這一種方法稱為配方法，利用配方法請解以下各題：
（1）按上面材料提示的方法填空：a2-4a=a2-4a+4-4a2-4a+4-4=（a-2）2-4（a-2）2-4．-a2+12a=-（a2-12a+36）+36-（a2-12a+36）+36=-（a-6）2+36-（a-6）2+36．
（2）探究：當a取不同的實數時在得到的代數式a2-4a的值中是否存在最小值？請說明理由．
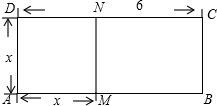
（3）應用：如圖．已知線段AB=6，M是AB上的一個動點，設AM=x,以AM為一邊作正方形AMND，再以MB、MN為一組鄰邊作長方形MBCN．問：當點M在AB上運動時，長方形MBCN的面積是否存在最大值？若存在，請求出這個最大值；否則請說明理由．
【考點】配方法的應用．
【答案】a2-4a+4-4；（a-2）2-4；-（a2-12a+36）+36；-（a-6）2+36
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：717引用：25難度：0.7
相似題
-
1．設x,y都是實數，請探究下列問題，
（1）嘗試：①當x=-2，y=1時，∵x2+y2=5，2xy=-4，∴x2+y2＞2xy.
②當x=1，y=2時，∵x2+y2=5，2xy=4，∴x2+y2＞2xy.
③當x=2，y=2.5時，∵x2+y2=10.25，2xy=10，∴x2+y2＞2xy.
④當x=3，y=3時，∵x2+y2=18，2xy=18，∴x2+y22xy.
（2）歸納：x2+y2與2xy有怎樣的大小關系？試說明理由．
（3）運用：求代數式的最小值．x2+4x2發布：2025/5/21 17:30:1組卷：188引用：2難度：0.5 -
2．關于x的一元二次方程新定義：若關于x的一元二次方程：a1（x-m）2+n=0與a2（x-m）2+n=0，稱為“同族二次方程”．如2（x-3）2+4=0與3（x-3）2+4=0就是“同族二次方程”．現有關于x的一元二次方程：2（x-1）2+1=0與（a+2）x2+（b-4）x+8=0是“同族二次方程”．那么代數式-ax2+bx+2015取的最大值是（ ）
發布：2025/5/24 6:0:2組卷：272引用：3難度：0.6 -
3．基本不等式的性質：一般地，對于a＞0，b＞0，我們有a+b≥2
，當且僅當a=b時等號成立．例如：若a＞0，則a+ab=6，當且僅當a=3時取等號，a+9a≥2a?9a的最小值等于6．根據上述性質和運算過程，若x＞1，則4x+9a的最小值是（ ）1x-1發布：2025/5/23 13:30:1組卷：839引用：6難度：0.4