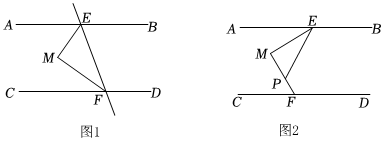【發(fā)現(xiàn)】如圖1，直線AB，CD被直線EF所截，EM平分∠AEF，F(xiàn)M平分∠CFE．若∠AEM=55°，∠CFM=35°，試判斷AB與CD平行嗎？并說明理由；
【探究】如圖2，若直線AB∥CD，點(diǎn)M在直線AB，CD之間，點(diǎn)E，F(xiàn)分別在直線AB，CD上，∠EMF=90°，P是MF上一點(diǎn)，且EM平分∠AEP．若∠CFM=60°，則∠AEP的度數(shù)為 60°60°；
【延伸】若直線AB∥CD，點(diǎn)E，F(xiàn)分別在直線AB，CD上，點(diǎn)M在直線AB，CD之間，且在直線EF的左側(cè)，P是折線E-M-F上的一個(gè)動(dòng)點(diǎn)，∠EMF=90°保持不變，移動(dòng)點(diǎn)P，使EM平分∠AEP或FM平分∠CFP．設(shè)∠CFP=α，∠AEP=β，請(qǐng)直接寫出α與β之間的數(shù)量關(guān)系．
【考點(diǎn)】平行線的判定與性質(zhì)．
【答案】60°
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/9 8:30:2組卷：511引用：4難度：0.4
相似題
-
1．填空并完成以下證明：
如圖，BD⊥AC于點(diǎn)D，EF⊥AC于點(diǎn)F，DM∥BC，∠1=∠2，求證：DM∥GF．
證明：∵BD⊥AC，EF⊥AC（已知）
∴∠BDF=∠EFC=90°（ ）
∴BD∥EF（ ）
∴∠1=（兩直線平行，同位角相等）
∵∠1=∠2（已知）
∴∠2=∠HFE（ ）
∴GF∥（內(nèi)錯(cuò)角相等，兩直線平行）
∵∥BC（已知）
∴DM∥GF（如果兩條直線都與第三條直線平行，那么這兩條直線也互相平行）發(fā)布：2025/6/9 14:30:1組卷：382引用：1難度：0.6 -
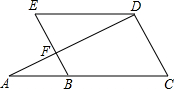2．已知：如圖，∠A=∠ADE，∠C=∠E．
（1）求證：BE∥CD；
（2）若∠EDC=3∠C，求∠C的度數(shù)．發(fā)布：2025/6/9 13:0:1組卷：1662引用：14難度：0.5 -
3．如圖，EF∥AD，∠1=∠2，∠BAC=85°．將求∠AGD的過程填寫完整．
解：∵EF∥AD，
∴∠2=∠3（ ）．
又∵∠1=∠2，
∴∠1=∠3（ ）．
∴AB∥DG（ ）．
∴∠BAC+∠AGD=180°（ ）．
∵∠BAC=85°，
∴∠AGD=95°．發(fā)布：2025/6/9 14:0:1組卷：4引用：1難度：0.7