如圖，已知△ABC是等腰三角形，AB=BC，點D，E，F(xiàn)分別在AB，BC，AC邊上，且DE=EF，∠DEF=∠ABC．
（1）如圖①，若∠A=60°，求證AD=BE；
（2）如圖②，若∠A=45°，如圖③，∠A=30°．請分別寫出線段AD和BE的數(shù)量關(guān)系，并對圖 ③進(jìn)行證明；
（3）在（2）的條件下，若CF=26，則AD=43或6243或62．
6
3
2
3
2
【考點】三角形綜合題．
【答案】4或6
3
2
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/2 9:0:1組卷：23引用：1難度：0.1
相似題
-
1．定義：我們把三角形被一邊中線分成的兩個三角形叫做“朋友三角形”．
性質(zhì)：“朋友三角形”的面積相等．
如圖1，在△ABC中，CD是AB邊上的中線．
那么△ACD和△BCD是“朋友三角形”，并且S△ACD=S△BCD．
應(yīng)用：如圖2，在直角梯形ABCD中，∠ABC=90°，AD∥BC，AB=AD=4，BC=6，點E在BC上，點F在AD上，BE=AF，AE與BF交于點O．
（1）求證：△AOB和△AOF是“朋友三角形”；
（2）連接OD，若△AOF和△DOF是“朋友三角形”，求四邊形CDOE的面積．
拓展：如圖3，在△ABC中，∠A=30°，AB=8，點D在線段AB上，連接CD，△ACD和△BCD是“朋友三角形”，將△ACD沿CD所在直線翻折，得到△A′CD，若△A′CD與△ABC重合部分的面積等于△ABC面積的，則△ABC的面積是 （請直接寫出答案）．14
發(fā)布：2025/6/3 22:30:1組卷：470引用：5難度：0.3 -
2．綜合與實踐
如圖1，在平面直角坐標(biāo)系中，點A，B的坐標(biāo)分別為A（-3，4），B（-3，0），將線段AB向下平移2個單位長度，再向右平移5個單位長度，得到線段CD，連接AC，BD，分別與y軸交于點E，F(xiàn)，點P為y軸上一點，連接PC，PD．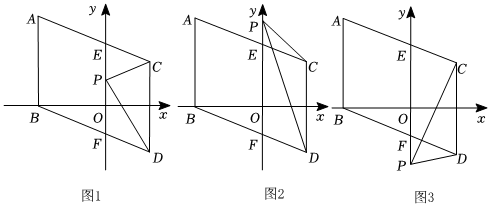
（1）如圖1，直接寫出點C與點D的坐標(biāo)：C（ ），D（ ）．
（2）如圖1，當(dāng)點P在線段EF上時，求證：∠ACP+∠BDP=∠CPD．
（3）①如圖2，當(dāng)點P在點E的上方時，直接寫出∠ACP、∠BDP、∠CPD的數(shù)量關(guān)系：；
②如圖3，當(dāng)點P在點F的下方時，直接寫出∠ACP、∠BDP、∠CPD的數(shù)量關(guān)系：．發(fā)布：2025/6/3 22:30:1組卷：36引用：1難度：0.2 -
3．已知在數(shù)軸上，從左往右依次有四個點A，C，D，B，其中點A，B對應(yīng)的數(shù)分別為-7和9．
（1）利用直尺和圓規(guī)作圖：如圖1，已知線段AC，CD，DB，在數(shù)軸上方，求作△ECD，使得EC=AC，ED=BD（只保留作圖痕跡）；
?（2）在（1）的條件下，在數(shù)軸上找一點F，直接作出直線EF，使得直線EF平分△ECD的周長；
（3）如圖2，在△ECD中，點G為CE中點，過點G的直線交ED于M，交CD的延長線于N，若DM=DN，求證：直線GN平分△ECD的周長；
（4）如圖3，若EC=ED，點P在邊CE上，點Q在邊ED上，且PQ平分△ECD的周長．
請問線段PQ的長是否為定值？若是定值，請說明理由；若不是定值，當(dāng)EP與EQ滿足什么關(guān)系時，線段PQ最短，并說明理由．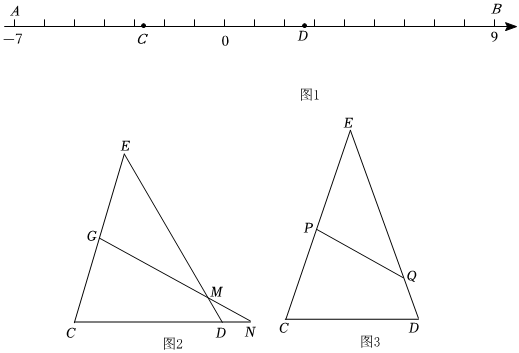
?發(fā)布：2025/6/3 22:30:1組卷：84引用：2難度：0.2