有一組等式，第1、第2、第3個等式分別為：1×12=1-12，2×23=2-23，3×34=3-34，按照這個規(guī)律，請寫出第n個等式（n≥1，且n為整數(shù)）：n×nn+1=n-nn+1n×nn+1=n-nn+1．
1
×
1
2
=
1
-
1
2
，
2
×
2
3
=
2
-
2
3
3
×
3
4
=
3
-
3
4
n
×
n
n
+
1
=
n
-
n
n
+
1
n
×
n
n
+
1
=
n
-
n
n
+
1
【考點】規(guī)律型：數(shù)字的變化類．
【答案】
n
×
n
n
+
1
=
n
-
n
n
+
1
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2025/5/29 14:30:2組卷：102引用：1難度：0.6
相似題
-
1．有一數(shù)值轉換器，原理如圖所示，若開始輸入x的值是8，可發(fā)現(xiàn)第一次輸出的結果是4，第二次輸出的結果是2，…，請你探索第2021次輸出的結果是 ．發(fā)布：2025/5/31 3:0:1組卷：84引用：1難度：0.6 -
2．計算：（1-2-3-…-2022）×（2+3+…+2023）-（1-2-3-…-2023）×（2+3+…+2022）的值（ ）
發(fā)布：2025/5/31 5:30:3組卷：436引用：3難度：0.5 -
3．如圖，階梯圖的每個臺階上都標著一個數(shù)．從下往上，第1個至第5個臺階上依次標有-3，-2，-1，1，4，且任意相鄰五個臺階上數(shù)的和都相等．
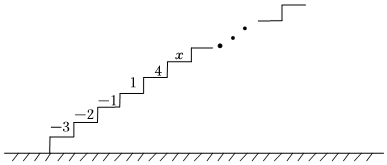
（1）求前5個臺階上的數(shù)的和；
（2）求第6個臺階上的數(shù)x；
（3）求從下往上前2023個臺階上的數(shù)的和；
（4）求第k次出現(xiàn)標“1”所在的臺階數(shù)．（用含k的式子表示）發(fā)布：2025/5/31 4:0:1組卷：120引用：2難度：0.5