如圖，△ABC是等腰三角形，∠C=90°，O是△ABC內(nèi)一點(diǎn)，點(diǎn)O到△ABC各邊的距離等于1，將△ABC繞點(diǎn)O順時針旋轉(zhuǎn)45°得到△A1B1C1，兩三角形的公共部分為多邊形KLMNPQ．
①證明：△AKL，△BMN，△CPQ都是等腰直角三角形．
②求△ABC與△A1B1C1公共部分的面積．
【答案】見試題解答內(nèi)容
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/29 9:0:1組卷：42引用：4難度：0.3
相似題
-
1．如圖，等腰直角三角形ABC中，∠C=90°，O是AB的中點(diǎn)，AD⊥BD，若，則OD的長為 ．AC=2發(fā)布：2025/5/30 8:0:2組卷：104引用：1難度：0.5 -
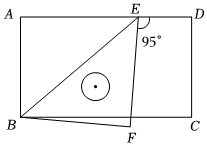2．如圖，把一塊含有45度角的直角三角板BEF放在長方形紙片ABCD上，使點(diǎn)E恰好落在AD邊上，若∠DEF=95°，則∠CBF=度．發(fā)布：2025/5/30 13:0:1組卷：78引用：1難度：0.6 -
3．如圖，在△ABC中，AB=AC，∠BAC=90°，AD為BC邊上的中線，若AD=1，則△ABC的面積為 ．發(fā)布：2025/5/30 8:30:2組卷：23引用：1難度：0.7