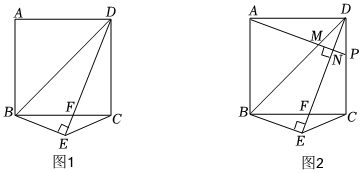
如圖1，在正方形ABCD中，DE⊥BE交BC于點F，連接BD，CE．
（1）探究∠EBD與∠ECB之間的數量關系，并證明；
（2）如圖2，過點A作AN⊥DE于點N，分別交BD，CD于點M，P，探究線段DN，BE，AN之間的數量關系，并證明．
?
【考點】正方形的性質；全等三角形的判定與性質．
【答案】（1）∠EBD+∠ECB=90°，理由見解析過程；
（2）AN=DN+BE，理由見解析過程．
（2）AN=DN+BE，理由見解析過程．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 21:0:1組卷：477引用：1難度：0.6
相似題
-
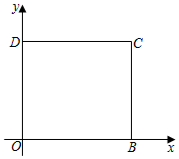1．如圖，四邊形OBCD是正方形，O，D兩點的坐標分別是（0，0），（0，5），點C在第一象限，則點C的坐標是 ．發布：2025/6/5 16:0:2組卷：339引用：8難度：0.9 -
2．勾股定理是人類最偉大的科學發現之一，在我國古算書《周髀算經》中早有記載．如圖1，以直角三角形的各邊為邊分別向外作正方形，再把較小的兩張正方形紙片按圖2的方式放置在最大正方形內．若知道．圖中陰影部分的面積，則一定能求出（ ）
發布：2025/6/5 14:0:1組卷：987引用：22難度：0.6 -
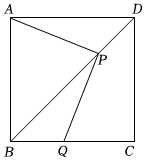3．如圖，已知正方形ABCD，邊長AB=6，點P為對角線BD上任一點，連接AP，過點P作PQ⊥AP交BC于點Q．
（1）求證：AP=PQ；
（2）若，求四邊形ABQP的面積．DP=2發布：2025/6/5 15:30:1組卷：937引用：3難度：0.4