小曼和他的同學組成了“愛琢磨”學習小組，有一次，他們碰到這樣一道題：“已知正方形ABCD，點E、F、G、H分別在邊AB、BC、CD、DA上，若EG⊥FH，則EG=FH．”為了解決這個問題，經過思考，大家給出了以下兩個方案：
方案一：過點A作AM∥HF交BC于點M，過點B作BN∥EG交CD于點N；
方案二：過點A作AM∥HF交BC于點M，過點A作AN∥EG交CD于點N．…
（1）對小曼遇到的問題，請在甲、乙兩個方案中任選一個加以證明（如圖（1））．
（2）如果把條件中的“正方形”改為“長方形”，并設AB=2，BC=3（如圖（2）），試探究EG、FH之間有怎樣的數量關系，并證明你的結論．
（3）如果把條件中的“EG⊥FH”改為“EG與FH的夾角為45°”，并假設正方形ABCD的邊長為1，FH的長為52（如圖（3）），試求EG的長度．
5
2
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：2329引用：5難度：0.1
相似題
-
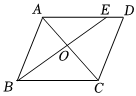1．如圖，在?ABCD，點E在AD上，且BE平分∠ABC，交AC于點O，若AB=3，BC=4，則=（ ）S△AOES△BOC發布：2025/5/23 18:30:2組卷：366引用：3難度：0.5 -
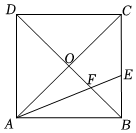2．如圖所示，正方形ABCD中，對角線AC、BD相交于點O，AE平分∠BAC，分別交BC、BD于E、F，下列結論：
①△ABF∽△ACE；
②BD=AD+BE；
③；BECE=23
④若△ABF的面積為1，則正方形ABCD的面積為．3+22
其中正確的結論的個數是（ ）發布：2025/5/23 19:0:2組卷：503引用：4難度：0.6 -
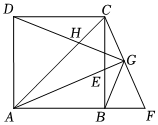3．如圖，四邊形ABCD為正方形，∠CAB的平分線交BC于點E，將△ABE繞點B順時針旋轉90°得到△CBF，延長AE交CF于點G，連接BG，DG，DG與AC相交于點H．有下列結論：①∠ACF=∠F；②G為△CBF的外心；③BG⊥DG；④．其中正確結論的序號是 ．AEDH=3發布：2025/5/23 19:0:2組卷：192引用：6難度：0.6