在△ABC中，∠BAC=100°，∠ABC=∠ACB，點D在直線BC上運動（不與點B、C重合），點E在射線AC上運動，且∠ADE=∠AED，設∠DAC=n°．
（1）如圖①，當點D在邊BC上，且n=40°時，則∠BAD=60°60°°，∠CDE=32°32°°；
（2）如圖②，當點D運動到點B的左側時，其他條件不變，請猜想∠BAD和∠CDE的數量關系，并說明理由；
（3）當點D運動到點C的右側時，其他條件不變，∠BAD和∠CDE還滿足（2）中的數量關系嗎？如果不變，請給予證明；如果改變，請說明理由．
【答案】60°；32°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：174引用：1難度：0.6
相似題
-
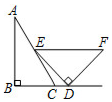1．一副直角三角尺如圖擺放，點D在BC的延長線上，EF∥BC，∠B=∠EDF=90°，∠A=30°，∠F=45°，則∠CED=．發布：2025/5/23 22:0:2組卷：360引用：5難度：0.5 -
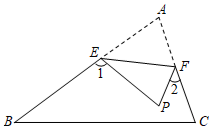2．如圖，已知點E，F分別在△ABC的邊AB，AC上，將∠A沿EF折疊，使點A落在點P的位置，已知∠A=70°，則∠1+∠2的度數為（ ）發布：2025/5/24 3:30:1組卷：526引用：4難度：0.7 -
3．如圖，把△ABC繞著點A順時針轉40°，得到△ADE，若點E恰好在邊BC上，AB⊥DE于點F，則∠BAE的大小是（ ）發布：2025/5/24 6:0:2組卷：588引用：5難度：0.6