如圖，陽光學校辦公樓AB的右邊有一建筑物CD，在建筑物CD離地面2米高的點E處觀測辦公樓頂A點，測得仰角∠AEM=22°，在離建筑物CD25米遠的F點觀測辦公樓頂A點，測得仰角∠AFB=45°（B，F(xiàn)，C在一條直線上）．求辦公樓AB的高度．（參考數(shù)據(jù)：sin22°=38，cos22°=1516，tan22°=25）
3
8
15
16
2
5
【考點】解直角三角形的應用-仰角俯角問題．
【答案】20米．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/8/9 8:0:9組卷：6引用：1難度：0.5
相似題
-
1．“創(chuàng)新實踐”小組想利用所學知識測量大樹AB的高度，因大樹底部有障礙物，無法直接測量到大樹底部的距離，他們制定了如下的測量方案：如圖所示，小麗通過調(diào)整測角儀的位置，在大樹周圍的點C處用測角儀測得大樹頂部A的仰角為45°（測角儀的高度忽略不計）．接著，小麗沿著BC方向向前走3米（即CD=3米），到達大樹在太陽光下的影子末端D處，此時小明測得小麗在太陽光下的影長DF為2米．已知小麗的身高DE為1.5米，B、C、D、F四點在同一直線上，AB⊥BF，DE⊥BF，求這棵大樹的高度AB．發(fā)布：2025/5/24 11:30:1組卷：107引用：3難度：0.5 -
2．飛機離水平地面的高度為3千米，在飛機上測得該水平地面上的目標A點的俯角為α，那么此時飛機與目標A點的距離為 千米．（用α的式子表示）
發(fā)布：2025/5/24 11:30:1組卷：130引用：3難度：0.6 -
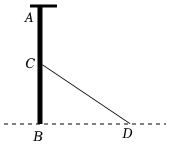3．如圖，電線桿AB的中點C處有一標志物，在地面D處測得標志物的仰角為32°．若D到電線桿底部B的距離為a,則電線桿AB的長為（ ）發(fā)布：2025/5/24 12:0:1組卷：133引用：1難度：0.7