綜合與實踐
綜合與實踐課上，老師讓同學們以“矩形的折疊”為主題開展數學活動．
（1）操作判斷
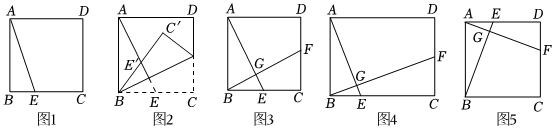
操作一：正方形透明紙片ABCD，點E在BC邊上，如圖1，連接AE，沿經過點B的直線折疊，使點E的對應點E'落AE在上，如圖2，把紙片展平，得到折痕BF，如圖3，折痕BF交AE于點G．
根據以上操作，請直接寫出圖3中AE與BF的位置關系：AE⊥BFAE⊥BF，BE與CF的數量關系：BE=CFBE=CF．
（2）遷移探究小華將正方形透明紙片換成矩形透明紙片，繼續探究，過程如下：
將矩形透明紙片ABCD按照（1）中的方式操作，得到折痕BF，折痕BF交AE于點G，如圖4．若mAB=nAD，改變點E在BC上的位置，那么BFAE的值是否能用含m,n的代數式表示？如果能，請推理BFAE的值，如果不能，請說明理由；
（3）拓展應用
如圖5，已知正方形紙片ABCD的邊長為2，動點E在AD邊上由點A向終點D勻速運動，動點F在DC邊上由點D向終點C勻速運動，動點E，F同時開始運動，且速度相同，連接AF，BE，交于點G，連接DG，則線段DG長度的最小值為：5-15-1，點G的運動路徑長度為：π2π2（直接寫出答案即可）．
BF
AE
BF
AE
5
-
1
5
-
1
π
2
π
2
【考點】相似形綜合題．
【答案】AE⊥BF；BE=CF；；
5
-
1
π
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/22 8:0:8組卷：187引用：1難度：0.2
相似題
-
1．在Rt△ABC中，∠BAC=90°，AB=AC，在Rt△ADE中，∠DAE=90°，2AD=AB，2AE=AC，連接DE，AN⊥BC，垂足為N，AM⊥DE，垂足為M．
（1）觀察猜想
圖①中，點D，E分別在AB，AC上時，的值為 ；BDCE的值為 ．BDMN
（2）探究證明
如圖②，將△ADE繞點A順時針旋轉，旋轉角為α（0°＜α＜360°），連接BD，CE，判斷問題（1）中的數量關系是否仍然存在，并證明；
（3）拓展延伸
在△ADE旋轉的過程中，設直線CE與BD相交于點F，若∠CAE=90°，AB=6，請直接寫出線段BF的長．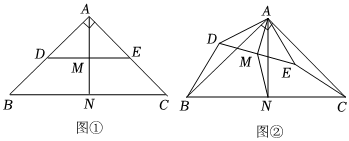
發布：2025/5/23 17:0:1組卷：518引用：1難度：0.1 -
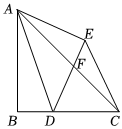2．如圖，△ABC中，∠B=90°，AB=BC，D為邊BC上一動點（不與B、C重合），CD和AD的垂直平分線交于點E，連接AD、AE、DE和CE，ED與AC相交于點F，設∠CAE=a.
（1）請用含a的代數式表示∠CED的度數；
（2）求證：△ABC∽△AED；
（3）若a=30°，求EF：BD的值．發布：2025/5/23 14:0:1組卷：77引用：1難度：0.1 -
3．問題提出
（1）如圖①，在△ABC中，點D、E、F分別為邊AB、AC、BC的中點，DE∥BC，BC=8，AF交DE于點G，則DG的長為 ；
問題探究
（2）如圖②，在等腰直角△ABC中，∠C=90°，AC=4，點D為線段CB上一動點（點D不與點B、C重合），以AD為腰且在AD的右側作等腰直角△ADF，∠ADF=90°，AB與FD交于點E，連接BF，求證：△ACD∽△ABF；
問題解決
（3）如圖是郊外一空地，為了美化生態環境，現要將這塊地打造成一個公園，在空地一側挖一個四邊形的人工湖CDQP，點P、Q分別在邊AB、AD上，且滿足PB=AQ，已知AB=AD，∠ACB=∠BAD=90°，AB=500m,BC=300m,為了滿足湖周邊的建設用地需要，人工湖的面積需盡可能小，設PB的長為x（m），四邊形CDQP的面積為S（m2）．
①求S與x之間的函數關系式；
②求人工湖面積的最小值及此時AQ的長．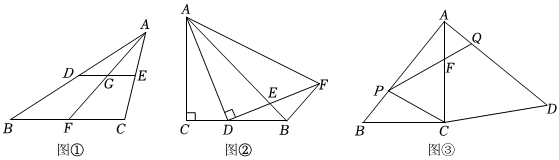
發布：2025/5/23 16:0:1組卷：259引用：1難度：0.3