【問題引入】：古希臘幾何學(xué)家海倫和我國南宋數(shù)學(xué)家秦九韶都曾提出利用三角形的三邊求面積的公式，為海倫-秦九韶公式，如果一個三角形的三邊長分別是a,b,c,記
p
=
a
+
b
+
c
2
，那么三角形面積為：
S
=
p
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
，在△ABC中，∠A，∠B，∠C所對的邊長分別為a,b,c若a=3，b=4，c=5，則△ABC的面積為6；
【問題探索】：如圖一，在△ABC中，設(shè)BC=a,AC=b,AB=c,
p
=
a
+
b
+
c
2
，⊙M是△ABC的內(nèi)切圓，⊙N分別與AC的延長線、AB的延長線以及線段BC均只有一個公共點，⊙M的半徑為m,⊙N的半徑為n.
（1）分析與證明：如圖二，連接MA、MB、MC，則△ABC被劃分為三個小三角形，用S表示△ABC的面積，
即S=S_△MBC+S_△MCA+S_△MAB那么S=p?m是否成立？請證明你的結(jié)論；
（2）理解與應(yīng)用：當∠A=60°，m=2，n=6時，求△ABC的面積．

【答案】（1）S=p?m成立，理由詳見解答；
（2）12

．

【解答】

【點評】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

發(fā)布：2024/6/27 10:35:59組卷：291引用：1難度：0.4

相似題

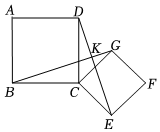1．如圖，正方形ABCD的邊長為4，正方形CEFG的邊長為
2
2
，將正方形CEFG繞點C旋轉(zhuǎn)，BG和DE相交于點K，則AK的最大值是
，連結(jié)BE，當點C正好是△BKE的內(nèi)心時，CK的長是
．
發(fā)布：2025/5/25 16:30:1組卷：1547引用：5難度：0.1
解析
2．在Rt△ACB中，∠ACB=90°，且AC=5，BC=12，則該三角形內(nèi)切圓的周長是
．
發(fā)布：2025/5/25 22:0:1組卷：150引用：1難度：0.7
解析
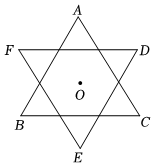3．如圖，正△ABC的邊長為6，將△ABC繞它的內(nèi)心O順時針旋轉(zhuǎn)60°得到△DEF，則它們重疊部分的面積是
．
發(fā)布：2025/5/26 2:30:2組卷：24引用：1難度：0.5
解析

相關(guān)試卷

1．如圖，正方形ABCD的邊長為4，正方形CEFG的邊長為22，將正方形CEFG繞點C旋轉(zhuǎn)，BG和DE相交于點K，則AK的最大值是 ，連結(jié)BE，當點C正好是△BKE的內(nèi)心時，CK的長是 ．