問題情景：如圖1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度數．
（1）天天同學看過圖形后立即回答出：∠APC=110°，請你補全他的推理依據．
如圖2，過點P作PE∥AB，
∵AB∥CD，
∴PE∥AB∥CD．（ 平行于同一條直線的兩條直線平行平行于同一條直線的兩條直線平行）
∴∠A+∠APE=180°．
∠C+∠CPE=180°．（ 兩直線平行同旁內角互補兩直線平行同旁內角互補）
∵∠PAB=130°，∠PCD=120°，
∴∠APE=50°，∠CPE=60°
∴∠APC=∠APE+∠CPE=110°．（ 等量代換等量代換）
問題遷移：
（2）如圖3，AD∥BC，當點P在A、B兩點之間運動時，∠ADP=∠α，∠BCP=∠β，求∠CPD與∠α、∠β之間有何數量關系？請說明理由．
（3）在（2）的條件下，如果點P在A、B兩點外側運動時（點P與點A、B、O三點不重合），請你直接寫出∠CPD與∠α、∠β之間的數量關系．
【考點】平行線的判定與性質．
【答案】平行于同一條直線的兩條直線平行；兩直線平行同旁內角互補；等量代換
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：3960引用：9難度：0.5
相似題
-
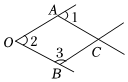1．如圖，一個由4條線段構成的“魚”形圖案，其中∠1=50°，∠2=50°，∠3=130°，找出圖中的平行線，∠ACB的度數，并說明理由．
解：OA∥BC，OB∥AC．
理由：∵∠1=50°，∠2=50°，
∴∠1=∠2（等量代換）
∴OB∥AC． （ ），
∴∠3+∠ACB=180°，（ ），
∴∠ACB=°，
∵∠2=50°，∠3=130°，
∴∠2+∠3=180°，
∴OA∥BC．（ ）．發布：2025/6/7 21:0:1組卷：680引用：6難度：0.9 -
2．下列結論中，正確的是（ ）
發布：2025/6/7 22:30:2組卷：1140引用：6難度：0.8 -
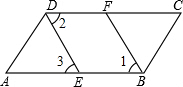3．如圖，∠ABC=∠ADC，BF、DE分別平分∠ABC與∠ADC，DE∥FB．求證：AB∥DC．
請根據條件進行推理，得出結論，并在括號內注明理由．
證明：∵BF、DE分別平分∠ABC與∠ADC，
∴∠1=∠ABC，∠2=12∠ADC．（12）
∵∠ABC=∠ADC，
∴．
∵DE∥FB
∴∠1=∠3，（）
∴∠2=．（等量代換）
∴AB∥CD．（）發布：2025/6/7 21:30:1組卷：637引用：4難度：0.3