數學興趣小組活動中，劉老師展示一個問題情境，供同學們探究：
問題情境：如圖，Rt△ABC中，∠C=90°，AB=10，AC=8，點P為斜邊AB上不與A，B重合的一個動點，過點P作PQ⊥AC于點Q，分別過P，Q作PD∥AC，QD∥AB，PD交QD于點D，請討論可能發現的結論．
以下是討論過程：
| 小明：我發現四邊形APDQ是平行四邊形． 理由：由作圖可知，PD∥AC，QD∥AB，∴四邊形APDQ是平行四邊形． 小亮：我和小明想法一樣，但還可以用全等三角形來解決． 理由：∵PD∥AC，QD∥AB，∴∠DPQ=∠AQP，∠DQP=∠APQ． 又∵PQ=QP，∴△PDQ≌△QAP．∴PD=AQ，QD=PA． ∴四邊形APDQ是平行四邊形． 小紅：我發現如果點D恰好落在BC上時，點P為AB的中點． |
請仔細閱讀討論過程，完成下述任務：
（1）小明推導四邊形APDQ是平行四邊形的依據是
兩組對邊分別平行的四邊形是平行四邊形
兩組對邊分別平行的四邊形是平行四邊形
，小亮推導四邊形APDQ是平行四邊形的依據是 兩組對邊分別相等的四邊形是平行四邊形
兩組對邊分別相等的四邊形是平行四邊形
，其中小亮得出△PDQ≌△QAP的依據是 ④
④
（填序號）；①SSS；②SAS；③AAS；④ASA；⑤HL（2）當點D恰好落在BC上時，請證明小紅的結論；
（3）若PD的中點為E，當點E恰好落在△ABC一邊的垂直平分線上時，直接寫出此時AP的長．
【考點】四邊形綜合題．
【答案】兩組對邊分別平行的四邊形是平行四邊形；兩組對邊分別相等的四邊形是平行四邊形；④
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/30 8:30:2組卷：159引用：2難度：0.1
相似題
-
1．【教材呈現】如圖是華師版九年級上冊數學教材第77頁的部分內容．
（1）【定理證明】請根據教材內容，結合圖①，寫出證明過程．猜想：如圖，在△ABC中，點D、E分別是AB與AC的中點．
根據畫出的圖形，可以猜想：
DE∥BC，且DE=BC．12
對此，我們可以用演繹推理給出證明．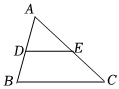
（2）【定理應用】如圖②，已知矩形ABCD中，AD=6，CD=4，點P在BC上從B向C移動，R、E、F分別是DC、AP、RP的中點，則EF=．
（3）【拓展提升】在△ABC中，AB=12，點E是AC的中點，過點A作∠ABC平分線的垂線，垂足為點F，連結EF，若EF=2，則BC=．
發布：2025/6/3 4:30:1組卷：259引用：2難度：0.2 -
2．如圖1，將一張矩形紙片ABCD沿著對角線BD向上折疊，頂點C落到點E處，BE交AD于點F．
（1）求證：△BAF≌△DEF；
（2）如圖2，過點D作DG∥BE，交BC于點G，連接FG交BD于點O．
①判斷四邊形BFDG的形狀，并說明理由；
②若AB=6，AD=8，求FG的長．發布：2025/6/3 5:30:1組卷：126引用：3難度：0.2 -
3．如圖1，在矩形ABCD中，AB=4，BC=10．點P是BC上的一個動點（不與點B、C重合），連接PA，過點P作PE⊥PA交CD于點E．
（1）設BP=x,CE=y,求y關于x的函數關系式；
（2）是否存在點P使得點E與點D重合，若存在，求出此時BP的長，若不存在，請說明理由；
（3）如圖2，連接BD，若PE∥BD，求CE的長．發布：2025/6/3 12:0:1組卷：13引用：1難度：0.3