(1)【問題初探】
蘇科版教材八年級下冊第九章《中心對稱圖形一一平行四邊形》復(fù)習(xí)題中有這樣的問題:如圖1正方形ABCD的邊長為2,∠EOF的頂點(diǎn)O在正方形ABCD兩條對角線的交點(diǎn)處,∠EOF=90°,將∠EOF繞點(diǎn)O旋轉(zhuǎn),∠EOF的兩邊分別與正方形ABCD的邊BC和CD交于點(diǎn)E和點(diǎn)F(點(diǎn)F與點(diǎn)C,D不重合),問:在旋轉(zhuǎn)過程中,四邊形OECF的面積會發(fā)生變化嗎?證明你的結(jié)論.
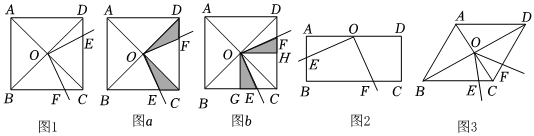
愛思考的浩浩和小航同學(xué)分別探究出了如下兩種解題思路:
浩浩:如圖a,充分利用正方形對角線垂直、相等且互相平分等性質(zhì)證明了△OEC≌△OFD,則S△OEC=S△OFD,那么S四邊形OECF=S△OEC+S△OCF=S△OFD+S△OCF=S△OCD,這樣,就實(shí)現(xiàn)了四邊形OECF的面積向△OCD面積的轉(zhuǎn)化;
小航:如圖b,也是考慮到正方形對角線的特征,過點(diǎn)O分別作OG⊥BC于點(diǎn)G,OH⊥CD于點(diǎn)H,證明△OGE≌△OHF,從而將四邊形OECF的面積轉(zhuǎn)化成了小正方形OGCH的面積.
通過他們的思路點(diǎn)撥,你認(rèn)為:S四邊形OECF=11(填一個數(shù)值),其實(shí),在這樣的旋轉(zhuǎn)變化過程中,線段CE與CF的和也是一個定值,為 22.
(2)【類比探究】
①如圖2,矩形ABCD中,AB=2,AD=4,點(diǎn)O是AD邊的中點(diǎn),∠EOF=90°,點(diǎn)E在AB上,點(diǎn)F在BC上,則四邊形EBFO的面積為 44;EB+BF=44;
②如圖3,若將(1)中的“正方形ABCD”改為“∠BCD=120°,邊長為8的菱形ABCD,其他條件不變,當(dāng)∠EOF=60°時,四邊形OECF的面積還是一個定值嗎?是,請求出來;不是,請說明理由;
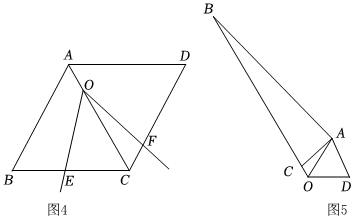
③如圖4,在②的條件下,當(dāng)點(diǎn)O在對角線AC上運(yùn)動,頂點(diǎn)O與B點(diǎn)的距離為7,且∠EOF旋轉(zhuǎn)至CF=1時,CE的長度為 4或24或2.
(3)【拓展延伸】
如圖5,∠BOD=α(α為鈍角),∠CAD=180°-α,∠BAC是鈍角,OA平分∠BOD,OD=34,OB=4,AB=13,OA=1,點(diǎn)C是OB上一點(diǎn),那么OC的長為 1414.
3
4
13
1
4
1
4
【考點(diǎn)】四邊形綜合題.
【答案】1;2;4;4;4或2;
1
4
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:1257引用:1難度:0.4
相似題
-
1.如圖1,點(diǎn)E為正方形ABCD內(nèi)一點(diǎn),∠AEB=90°,現(xiàn)將Rt△ABE繞點(diǎn)B按順時針方向旋轉(zhuǎn)90°,得到△CBE′(點(diǎn)A的對應(yīng)點(diǎn)為點(diǎn)C),延長AE交CE′于點(diǎn)F.

(1)如圖1,求證:四邊形BEFE′是正方形;
(2)連接DE,
①如圖2,若DA=DE,求證:F為CE′的中點(diǎn);
②如圖3,若AB=15,CF=3,試求DE的長.發(fā)布:2025/6/8 22:30:1組卷:532引用:2難度:0.4 -
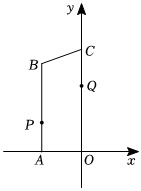 2.如圖在平面直角坐標(biāo)系中,A(-8,0),C(0,26),AB∥y軸且AB=24,點(diǎn)P從點(diǎn)A出發(fā),以1個單位長度/s的速度向點(diǎn)B運(yùn)動;點(diǎn)Q從點(diǎn)C同時出發(fā),以2個單位長度/s的速度向點(diǎn)O運(yùn)動,規(guī)定其中一個動點(diǎn)到達(dá)端點(diǎn)時,另一個動點(diǎn)也隨之停止運(yùn)動,設(shè)運(yùn)動的時間為t秒.
2.如圖在平面直角坐標(biāo)系中,A(-8,0),C(0,26),AB∥y軸且AB=24,點(diǎn)P從點(diǎn)A出發(fā),以1個單位長度/s的速度向點(diǎn)B運(yùn)動;點(diǎn)Q從點(diǎn)C同時出發(fā),以2個單位長度/s的速度向點(diǎn)O運(yùn)動,規(guī)定其中一個動點(diǎn)到達(dá)端點(diǎn)時,另一個動點(diǎn)也隨之停止運(yùn)動,設(shè)運(yùn)動的時間為t秒.
(1)當(dāng)四邊形BCQP是平行四邊形時,求t的值;
(2)當(dāng)PQ=BC時,求t的值;
(3)當(dāng)PQ恰好垂直平分BO時,求t的值.發(fā)布:2025/6/8 22:30:1組卷:177引用:3難度:0.3 -
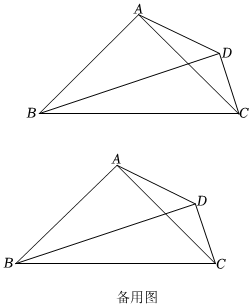 3.如圖,四邊形ABCD中,已知∠BAC=∠BDC=90°,且AB=AC.
3.如圖,四邊形ABCD中,已知∠BAC=∠BDC=90°,且AB=AC.
(1)求證:∠ABD=∠ACD;
(2)記△ABD的面積為S1,△ACD的面積為S2.
①求證:S1-S2=AD2;12
②過點(diǎn)B作BC的垂線,過點(diǎn)A作BC的平行線,兩直線相交于M,延長BD至P,使得DP=CD,連接MP.當(dāng)MP取得最大值時,求∠CBD的大小.發(fā)布:2025/6/8 23:0:1組卷:308引用:4難度:0.1


