當前位置：試卷中心 > 試卷詳情

2021-2022學年江蘇省淮安市淮陰區開明中學八年級（下）期中數學試卷

發布：2024/4/20 14:35:0

一、選擇題（本大題共8小題，每小題3分，共24分。請將答案涂到答題紙上）

1．下列圖形中，是中心對稱圖形的是（　　）
A． B． C． D．
組卷：40引用：1難度：0.8
解析
2．若分式
x
-
1
x
+
1
的值為零，則x的值是（　　）
A．1 B．-1 C．±1 D．0
組卷：404引用：11難度：0.9
解析
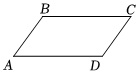3．如圖，在平行四邊形中ABCD，∠A=45°，則∠C=（　　）
A．35° B．45° C．55° D．65°
組卷：44引用：3難度：0.6
解析
4．下列分式中屬于最簡分式的是（　　）
A．
x
2
-
9
x
+
3
B．
x
-
1
2
x
-
2
C．
2
6
y
+
12
D．
x
+
2
y
+
2
組卷：94引用：1難度：0.8
解析
5．將分式
xy
x
+
y
中的x,y的值都變為原來的2倍，則該分式的值（　　）
A．變為原來的2倍 B．變為原來的4倍
C．不變 D．變為原來的一半
組卷：190引用：5難度：0.7
解析

6．下列說法錯誤的是（　　）

A．對角線互相平分的四邊形是平行四邊形

B．對角線互相垂直的四邊形是菱形

C．對角線相等的平行四邊形是矩形

D．有一組鄰邊相等且有一個角是直角的平行四邊形是正方形

組卷：151引用：3難度：0.7

解析

7．已知反比例函數y=
m
x
的圖象分布在二、四象限，那么一次函數y=mx+2的圖象不經過哪個象限（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：58引用：1難度：0.7
解析
8．已知甲、乙兩地相距s（km），汽車從甲地勻速行駛到乙地，則汽車行駛的時間t（h）與行駛速度v（km/h）的函數關系圖象大致是（　　）
A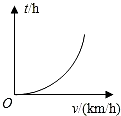． B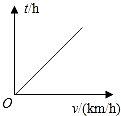． C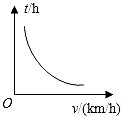． D．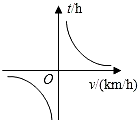
組卷：959引用：89難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共9小題，共72分。請將解答過程填寫在答題紙上）

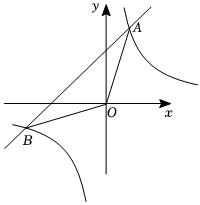24．如圖，一次函數y=kx+b的圖象與反比例函數y=
m
x
的圖象交于A（1，3），B（-3，n）兩點．
（1）求反比例函數和一次函數的表達式；
（2）求△AOB的面積；
（3）根據圖象直接寫出一次函數值小于反比例函數值的x的取值范圍；
（4）若點P在x軸上，點Q在反比例函數y=
m
x
的圖象上，當以A、B、P、Q為頂點的四邊形為平行四邊形時，直接寫出點Q的坐標：
．
組卷：208引用：1難度：0.1
解析
25．（1）【問題初探】
蘇科版教材八年級下冊第九章《中心對稱圖形一一平行四邊形》復習題中有這樣的問題：如圖1正方形ABCD的邊長為2，∠EOF的頂點O在正方形ABCD兩條對角線的交點處，∠EOF=90°，將∠EOF繞點O旋轉，∠EOF的兩邊分別與正方形ABCD的邊BC和CD交于點E和點F（點F與點C，D不重合），問：在旋轉過程中，四邊形OECF的面積會發生變化嗎？證明你的結論．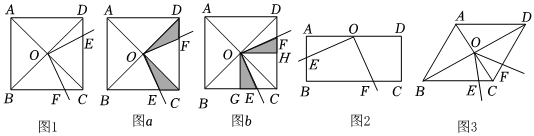

愛思考的浩浩和小航同學分別探究出了如下兩種解題思路：
浩浩：如圖a,充分利用正方形對角線垂直、相等且互相平分等性質證明了△OEC≌△OFD，則S_△OEC=S_△OFD，那么S_{四邊形OECF}=S_△OEC+S_△OCF=S_△OFD+S_△OCF=S_△OCD，這樣，就實現了四邊形OECF的面積向△OCD面積的轉化；
小航：如圖b,也是考慮到正方形對角線的特征，過點O分別作OG⊥BC于點G，OH⊥CD于點H，證明△OGE≌△OHF，從而將四邊形OECF的面積轉化成了小正方形OGCH的面積．
通過他們的思路點撥，你認為：S_{四邊形OECF}=
（填一個數值），其實，在這樣的旋轉變化過程中，線段CE與CF的和也是一個定值，為
．
（2）【類比探究】
①如圖2，矩形ABCD中，AB=2，AD=4，點O是AD邊的中點，∠EOF=90°，點E在AB上，點F在BC上，則四邊形EBFO的面積為
；EB+BF=
；
②如圖3，若將（1）中的“正方形ABCD”改為“∠BCD=120°，邊長為8的菱形ABCD，其他條件不變，當∠EOF=60°時，四邊形OECF的面積還是一個定值嗎？是，請求出來；不是，請說明理由；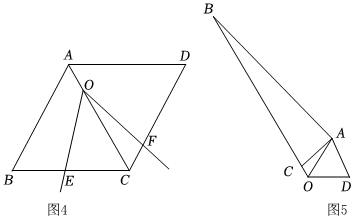

③如圖4，在②的條件下，當點O在對角線AC上運動，頂點O與B點的距離為7，且∠EOF旋轉至CF=1時，CE的長度為
．
（3）【拓展延伸】
如圖5，∠BOD=α（α為鈍角），∠CAD=180°-α，∠BAC是鈍角，OA平分∠BOD，OD=
3
4
，OB=4，AB=
13
，OA=1，點C是OB上一點，那么OC的長為
．
組卷：1255引用：1難度：0.4
解析