閱讀下面的題目及分析過程，并按要求進行證明．
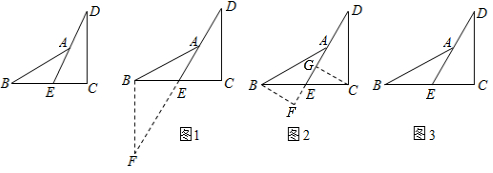
已知：如圖，點E是BC的中點，點A在DE上，且∠BAE=∠CDE．
求證：AB=CD．
分析：證明兩條線段相等，常用的方法是應用全等三角形或等腰三角形的判定和性質，觀察本題中要證明的兩條線段，它們不在同一個三角形中，且它們分別所在的兩個三角形也不全等，因此，要證AB=CD，必須添加適當的輔助線，構造全等三角形或等腰三角形．
（1）現給出如下兩種添加輔助線的方法，請任意選出其中一種，對原題進行證明．
①如圖1，延長DE到點F，使EF=DE，連接BF；
②如圖2，分別過點B、C作BF⊥DE，CG⊥DE，垂足分別為點F，G．
（2）請你在圖3中添加不同于上述的輔助線，并對原題進行證明．
【考點】三角形綜合題．
【答案】（1）（2）（3）證明見解答．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1521引用：3難度：0.4
相似題
-
1．如圖（1），已知CA=CB，CD=CE，且∠ACB=∠DCE，將△DCE繞C點旋轉（A、C、D三點在同一直線上除外）．
（1）求證：△ACD≌△BCE；
（2）在△DCE繞C點旋轉的過程中，若ED、AB所在的直線交于點F，當點F為邊AB的中點時，如圖2所示．求證：∠ADF=∠BEF（提示：利用類倍長中線方法添加輔助線）；
（3）在（2）的條件下，求證：AD⊥CD．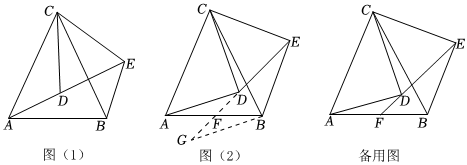
發布：2025/6/5 4:0:1組卷：1141引用：12難度：0.3 -
2．如圖，△ABC為等邊三角形，直線l經過點C，在l上位于C點右側的點D滿足∠BDC=60°．
（1）如圖1，在l上位于C點左側取一點E，使∠AEC=60°，求證：△AEC≌△CDB；
（2）如圖2，點F、G在直線l上，連接AF，在l上方作∠AFH=120°，且AF=HF，∠HGF=120°，求證：HG+BD=CF；
（3）在（2）的條件下，當A、B位于直線l兩側，其余條件不變時（如圖3），線段HG、CF、BD的數量關系為．
發布：2025/6/5 5:0:1組卷：2123引用：6難度：0.1 -
3．已知，如圖1，△ABC中，AC=BC，D，E分別是線段AC，AB的中點，且滿足DE∥BC，BC=2DE，P為邊AB上一動點，連接DP，以DP為一邊在右側作△DPQ，使DP=DQ，且∠PDQ=∠ACB，連接EQ并延長交直線BC于點H．
（1）求證：△APD≌△EQD；
（2）若∠ACB=120°，判斷線段BC與線段CH的數量關系，并說明理由；
（3）在（2）的條件下，延長DQ交BC于點G，若AC=6，當△HQG為直角三角形時，求AP的長度．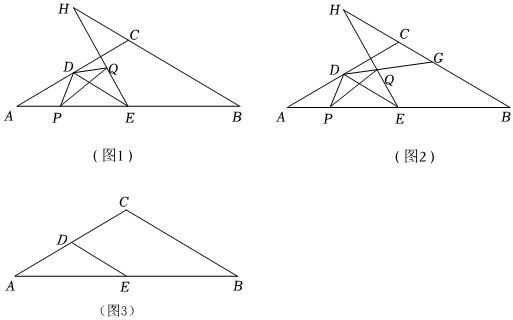
發布：2025/6/5 3:30:1組卷：195引用：1難度：0.1