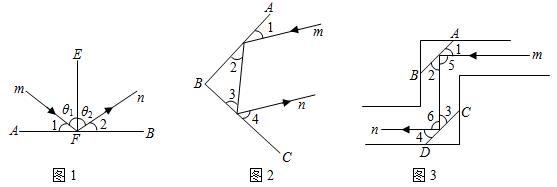
圖1展示了光線反射定律：EF是鏡面AB的垂線，一束光線m射到平面鏡AB上，被AB反射后的光線為n,則入射光線m,反射光線n與垂線EF所夾的銳角θ1=θ2．
（1）在圖1中，證明：∠1=∠2．
（2）圖2中，AB，BC是平面鏡，入射光線m經(jīng)過兩次反射后得到反射光線n,已知∠1=30°，∠4=60°，判斷直線m與直線n的位置關(guān)系，并說明理由．
（3）圖3是潛望鏡工作原理示意圖，AB，CD是平行放置的兩面平面鏡．請(qǐng)解釋進(jìn)入潛望鏡的光線m為什么和離開潛望鏡的光線n是平行的？
【考點(diǎn)】平行線的判定與性質(zhì)．
【答案】（1）見解析；
（2）直線m∥直線n，理由見解析；
（3）見解析．
（2）直線m∥直線n，理由見解析；
（3）見解析．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：523引用：8難度：0.5
相似題
-
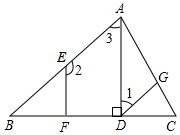1．如圖，已知AD⊥BC，垂足為點(diǎn)D，EF⊥BC，垂足為點(diǎn)F，∠1+∠2=180°．請(qǐng)?zhí)顚憽螩GD=∠CAB的理由．
∵AD⊥BC，EF⊥BC，
∴∠ADC=90°，∠EFC=90° （ ），
∴∠ADC=∠EFC，
∴AD∥（ ），
∴∠+∠2=180°（ ），
∵∠1+∠2=180°，
∴∠=∠（ ），
∴DG∥（ ），
∴∠CGD=∠CAB．發(fā)布：2025/6/8 20:0:1組卷：863引用：12難度：0.5 -
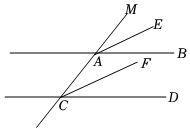2．如圖，若直線AB∥CD，AE，CF分別是∠MAB和∠MCD的角平分線，求證：AE∥CF．
證明：∵AB∥CD（已知）
∴∠MAB=（ ）．
∵AE，CF分別是∠MAB和∠MCD的角平分線（已知），
∴=，12∠MAB（角平分線的定義）．∠MCF=12
∴∠MAE=（等量代換）．
∴AE∥CF （ ）．發(fā)布：2025/6/8 20:30:2組卷：160引用：2難度：0.8 -
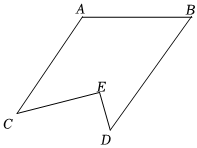3．如圖，AC，BD被AB所截，E為AB外一點(diǎn)，連接CE，ED，已知∠A=（90+x）°，∠B=（90-x）°，∠CED=90°，2∠C-∠D=α°．
（1）判斷AC與BD的位置關(guān)系，并說明理由；
（2）當(dāng)α=30°時(shí)，求∠C，∠D的度數(shù)；
（3）求∠C，∠D的度數(shù)（用含α的式子表示）．發(fā)布：2025/6/8 19:30:1組卷：83引用：2難度：0.7