問題背景：
如圖1所示，在四邊形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F(xiàn)分別是BC，CD上的點(diǎn)，且∠EAF=60°，探究圖中線段BE，EF，F(xiàn)D之間的數(shù)量關(guān)系．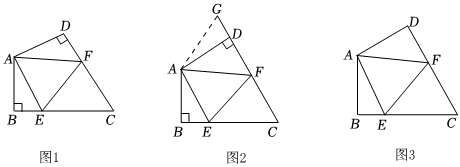
（1）小王同學(xué)探究此問題的方法是延長FD到點(diǎn)G，使DG=BE，連接AG，如圖2所示，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結(jié)論，他的結(jié)論應(yīng)是 EF=BE+DFEF=BE+DF；
（2）如圖所示，若在四邊形ABCD中，AB=AD，∠B+∠D=180°，E，F(xiàn)分別是BC，CD上的點(diǎn)，且∠EAF=12∠BAD．上述結(jié)論是否仍然成立？請說明理由．
∠
EAF
=
1
2
∠
BAD
【考點(diǎn)】全等三角形的判定與性質(zhì)；角平分線的性質(zhì)．
【答案】EF=BE+DF
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：420引用：2難度：0.5
相似題
-
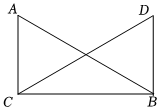1．如圖，AC⊥CB，DB⊥CB，垂足分別為C、B，AB=DC，求證：∠A=∠D．發(fā)布：2025/5/23 1:0:1組卷：162引用：9難度：0.5 -
2．如圖，在△ABC中，∠ABC=45°，CD⊥AB，BE⊥AC，垂足分別為D，E，F(xiàn)為BC中點(diǎn)，BE與DF，DC分別交于點(diǎn)G，H，∠ABE=∠CBE．
（1）線段BH與AC相等嗎？若相等給予證明，若不相等請說明理由；
（2）求證：BG2-GE2=EA2．發(fā)布：2025/5/23 0:0:1組卷：3459引用：27難度：0.1 -
3．我國的紙傘制作工藝十分巧妙，如圖，傘不管是張開還是收攏，傘柄AP始終平分同一平面內(nèi)兩條傘骨所成的角∠BAC，且AB=AC，AE=AF，從而保證傘圈D沿著傘柄滑動(dòng)．
（1）求證：△AED≌△AFD．
（2）當(dāng)傘撐開后，我們發(fā)現(xiàn)B，D，C在同一條直線止，已知AB=60cm,AD=36cm,兩個(gè)身體寬度45cm的人撐傘并排站立，兩人之間間隔10cm,請問他們是否會(huì)淋到雨？并說明理由．發(fā)布：2025/5/23 2:0:6組卷：210引用：2難度：0.5