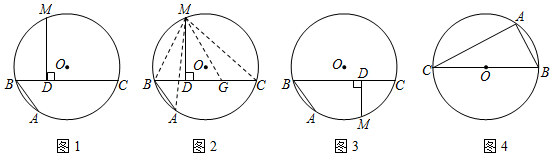
【問題呈現】阿基米德折弦定理:阿基米德(archimedes,公元前287-公元前212年,古希臘)是有史以來最偉大的數學家之一,他與牛頓、高斯并稱為三大數學王子.如圖1,AB和BC是⊙O的兩條弦(即折線ABC是圓的一條折弦),BC>AB,點M是?ABC的中點,則從M向BC所作垂線的垂足D是折弦ABC的中點,即CD=DB+BA.下面是運用“截長法”證明CD=DB+BA的部分證明過程.
證明:如圖2,在CD上截取CG=AB,連接MA、MB、MC和MG.
∵M是?ABC的中點,
∴MA=MC,
又∵∠A=∠C,BA=GC,
∴△MAB≌△MCG,
∴MB=MG,
又∵MD⊥BC,
∴BD=DG,
∴AB+BD=CG+DG即CD=DB+BA.
【理解運用】如圖1,AB、BC是⊙O的兩條弦,AB=4,BC=6,點M是?ABC的中點,MD⊥BC于點D,則BD=11;
【變式探究】如圖3,若點M是?AC的中點,【問題呈現】中的其他條件不變,判斷CD、DB、BA之間存在怎樣的數量關系?并加以證明.
【實踐應用】如圖4,BC是⊙O的直徑,點A圓上一定點,點D圓上一動點,且滿足∠DAC=45°,若AB=6,⊙O的半徑為5,則AD=72或272或2.
?
ABC
?
ABC
?
ABC
?
AC
2
2
2
2
【考點】圓的綜合題.
【答案】1;7或
2
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/24 15:30:1組卷:1264引用:8難度:0.2
相似題
-
1.已知⊙O的直徑AB=2,弦AC與弦BD交于點E,且OD⊥AC,垂足為點F.
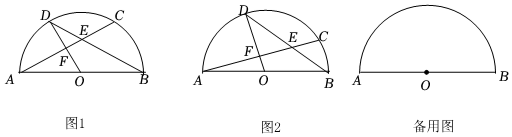
(1)如圖1,若AC=BD,求線段DE的長.
(2)如圖2,若DE:BE=3:2,求∠ABD的正切值.
(3)連結BC,CD,DA,若BC是⊙O的內接正n邊形的一邊,CD是⊙O的內接正2n邊形的一邊,求△ACD的面積.發布:2025/5/24 21:30:1組卷:239引用:1難度:0.3 -
2.在Rt△ABC中,∠C=90°.
(1)如圖①,點O在斜邊AB上,以點O為圓心,OB長為半徑的圓交AB于點D,交BC于點E,與邊AC相切于點F.求證:∠1=∠2;
(2)在圖②中作⊙M,使它滿足以下條件:
①圓心在邊AB上;②經過點B;③與邊AC相切.
(尺規作圖,只保留作圖痕跡,不要求寫出作法)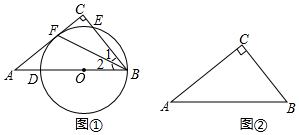 發布:2025/5/24 21:30:1組卷:833引用:9難度:0.3
發布:2025/5/24 21:30:1組卷:833引用:9難度:0.3 -
3.如圖1,△AOB是邊長為5的等邊三角形,弧長為π的扇形POQ按圖1擺放,使扇形的半徑OP,OQ分別落在OA,OB上.
(1)求OP的長;
(2)若△AOB不動,讓扇形POQ繞點O逆時針旋轉,得到扇形P′OQ′,如圖2,連接線段AP′,BQ′,設旋轉角為α(0°<α<90°).
①求證:AP′=BQ′,并求當AP′與弧P′Q′相切時cosα的值;
②如圖3,若α=60°,連接PP′,P′Q′,直接判斷四邊形OPP′Q′的形狀.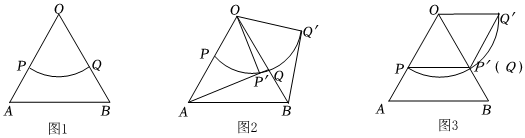 發布:2025/5/24 22:30:1組卷:57引用:1難度:0.2
發布:2025/5/24 22:30:1組卷:57引用:1難度:0.2
相關試卷


