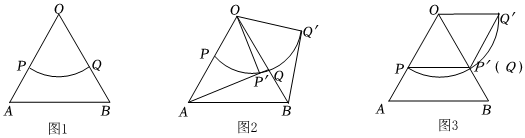
如圖1，△AOB是邊長為5的等邊三角形，弧長為π的扇形POQ按圖1擺放，使扇形的半徑OP，OQ分別落在OA，OB上．
（1）求OP的長；
（2）若△AOB不動，讓扇形POQ繞點O逆時針旋轉，得到扇形P′OQ′，如圖2，連接線段AP′，BQ′，設旋轉角為α（0°＜α＜90°）．
①求證：AP′=BQ′，并求當AP′與弧P′Q′相切時cosα的值；
②如圖3，若α=60°，連接PP′，P′Q′，直接判斷四邊形OPP′Q′的形狀．
【考點】圓的綜合題．
【答案】（1）OP=3；
（2）①cosα=；
②菱形．
（2）①cosα=
3
5
②菱形．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/24 22:30:1組卷：57引用：1難度：0.2
相似題
-
1．定義：如果一個四邊形的一組對角互余，那么我們稱這個四邊形為“對角互余四邊形”．
（1）如圖1，在“對角互余四邊形”ABCD中，AD=CD，BD=6.5，∠ABC+∠ADC=90°，AB=4，CB=3，求四邊形ABCD的面積．
（2）如圖2，在四邊形ABCD中，連接AC，∠BAC=90°，點O是△ACD外接圓的圓心，連接OA，∠OAC=∠ABC．求證：四邊形ABCD是“對角互余四邊形”；
（3）在（2）的條件下，如圖3，已知AD=a,DC=b,AB=3AC，連接BD，求BD2的值．（結果用帶有a,b的代數式表示）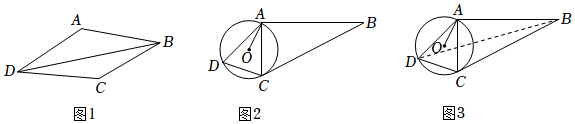
發布：2025/5/25 2:0:6組卷：305引用：2難度：0.3 -
2．【根底鞏固】
（1）如圖，在△ABC中，D為AB上一點，∠ACD=∠B．求證：AC2=AD?AB．
【嘗試應用】
（2）如圖2，在菱形ABCD中，E，F分別為BC，DC上的點，且∠EAF=∠BAD，射線AE交DC的延長線于點M，射線AF交BC的延長線于點N．若AF=4，CF=2，AM=10．12
求：①CM的長；
②FN的長．
【拓展進步】
（3）如圖3，在菱形ABCD中，AB=6，∠B=60°，以點B為圓心作半徑為3的圓，其中點P是圓上的動點，請直接寫出PD+PC的最小值．12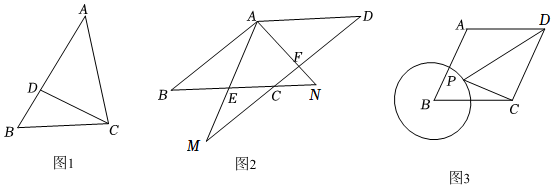
發布：2025/5/25 2:30:1組卷：870引用：2難度：0.1 -
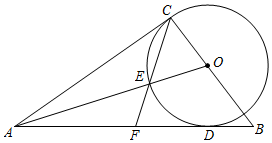3．如圖，在△ABC的邊BC上取一點O，以O為圓心，OC為半徑畫⊙O，⊙O與邊AB相切于點D，AC=AD，連接OA交⊙O于點E，連接CE，并延長交線段AB于點F．
（1）求證：AC是⊙O的切線；
（2）若AB=10，tanB=，求⊙O的半徑；43
（3）若F是AB的中點，試探究BD+CE與AF的數量關系并說明理由．發布：2025/5/25 3:0:2組卷：6113引用：25難度：0.2