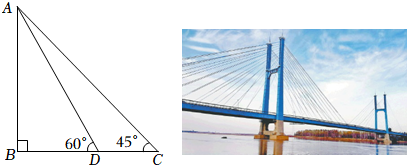
勝利黃河大橋猶如一架巨大的豎琴，凌駕于滔滔黃河之上，使黃河南北“天塹變通途”．已知主塔AB垂直于橋面BC于點(diǎn)B，其中兩條斜拉索AD、AC與橋面BC的夾角分別為60°和45°，兩固定點(diǎn)D、C之間的距離約為33m,求主塔AB的高度（結(jié)果保留整數(shù)，參考數(shù)據(jù)：2≈1.41，3≈1.73）．
2
3
【考點(diǎn)】解直角三角形的應(yīng)用；勾股定理的應(yīng)用．
【答案】78m．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：2863引用：10難度：0.5
相似題
-
1．如圖，小明在某天15：00時(shí)測(cè)量某樹(shù)的影長(zhǎng)時(shí)，日照的光線(xiàn)與地面的夾角∠ACB=60°，當(dāng)他在17：00時(shí)測(cè)量該樹(shù)的影長(zhǎng)時(shí)，日照的光線(xiàn)與地面的夾角∠ADB=30°，若兩次測(cè)得的影長(zhǎng)之差CD長(zhǎng)為6m,則樹(shù)的高度為m.3發(fā)布：2025/5/24 7:0:1組卷：824引用：5難度：0.7 -
2．下面是華師版九年級(jí)上冊(cè)數(shù)學(xué)教材第103頁(yè)的部分內(nèi)容．
請(qǐng)根據(jù)教材提示，結(jié)合圖①，寫(xiě)出完整的證明過(guò)程．
例2如圖，在Rt△ABC中，∠ACB=90°，CD是斜邊AB上的中線(xiàn)．
求證：．CD=12AB
證明：延長(zhǎng)CD至點(diǎn)E，使DE=CD，連結(jié)AE、BE．
（1）如圖②，直角三角形ABC紙片中，∠ACB=90°，點(diǎn)D是AB邊上的中點(diǎn)，連結(jié)CD，將△ACD沿CD折疊，點(diǎn)A落在點(diǎn)E處，此時(shí)恰好有CE⊥AB．若BC=3，那么CE=．
（2）如圖③，在△ABC中，AD是BC邊上的高線(xiàn)，CE是AB邊上的中線(xiàn)，G是CE的中點(diǎn)，CD=AE．若AB=10，DG=2，則cos∠BCE=．
發(fā)布：2025/5/24 7:30:1組卷：555引用：5難度：0.1 -
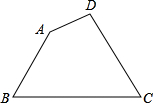3．如圖2，有一塊四邊形的鐵板余料ABCD，經(jīng)測(cè)量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=，若要從這塊余料中裁出頂點(diǎn)M、N在邊BC上且面積最大的矩形PQMN，則該矩形的面積為cm2．43發(fā)布：2025/5/24 8:30:1組卷：1218引用：2難度：0.1