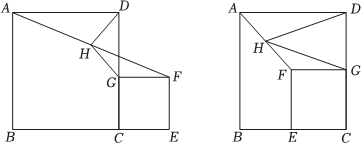
綜合實踐：如圖，四邊形ABCD，CEFG都是正方形，點E在BC延長線上，且CE＜BC，連接AF，點H為AF中點，連接HD，HG，試探究HD，HG的數量關系？同學們經過思考后，交流了自己的想法：
小琪：“通過觀察和度量，可以發現線段HD，HG存在某種數量關系；”
小偉：“探究HD，HG的數量關系，可以延長GH，構造與△HGF全等的三角形，經過進一步推理再證明．”
（1）猜想：HD與HG的數量關系，并說明理由；
（2）將正方形CEFG沿CD翻折到如圖位置（點E在BC上），此時（1）中的結論還成立嗎？請說明理由．
?
【考點】四邊形綜合題．
【答案】（1）DH=DG，理由見解析；
（2）DH=DG，理由見解析．
（2）DH=DG，理由見解析．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/14 8:0:9組卷：246引用：1難度：0.6
相似題
-
1．在平面直角坐標系xOy中，對于點P（x1，y1），給出如下定義：當點Q（x2，y2）滿足x1?x2=y1?y2時，稱點Q是點P的等積點．已知點P（1，2）．
（1）在Q1（2，1），Q2（-4，-1），Q3（8，2）中，點P的等積點是 ．
（2）點Q是P點的等積點，點C在x軸上，以O，P，Q，C為頂點的四邊形是平行四邊形，求點C的坐標．
（3）已知點和點M（4，m），點N是以點M為中心，邊長為2且各邊與坐標軸平行的正方形T上的任意一點，對于線段BN上的每一點A，在線段PB上都存在一個點R使得A為R的等積點，直接寫出m的取值范圍．B（1，12）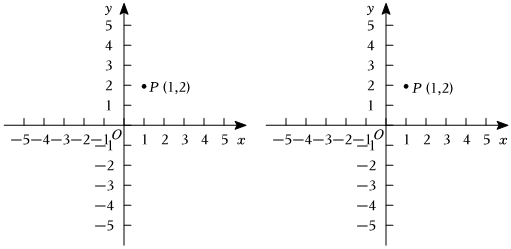
發布：2025/6/10 1:0:1組卷：129引用：1難度：0.9 -
2．感知：數學課上，老師給出了一個模型：如圖1，點A在直線DE上，且∠BDA=∠BAC=∠AEC=90°，像這種一條直線上的三個頂點含有三個相等的角的模型我們把它稱為“一線三等角“模型．
應用：（1）如圖2，Rt△ABC中，∠ACB=90°，CB=CA，直線ED經過點C，過A作AD⊥ED于點D，過B作BE⊥ED于點E．求證：△BEC≌△CDA．
（2）如圖3，在△ABC中，D是BC上一點，∠CAD=90°，AC=AD，∠DBA=∠DAB，AB=2，求點C到AB邊的距離．3
（3）如圖4，在?ABCD中，E為邊BC上的一點，F為邊AB上的一點．若∠DEF=∠B，AB=10，BE=6，求的值．EFDE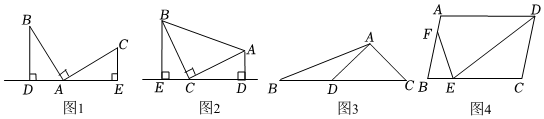
發布：2025/6/10 1:30:1組卷：2068引用：10難度：0.4 -
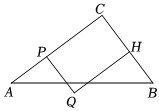3．如圖，在△ABC中，∠C=90°，AC=4，BC=3，點P從A出發，沿AC方向以每秒1個單位長度的速度向終點C運動．當點P不與點A、C重合時，將線段AP繞點P逆時針旋轉90°，得到線段PQ，以PC、PQ為邊作矩形PQHC．點H恰好落在直線BC上，設矩形PQHC與△ABC重疊部分的圖形面積為S（平方單位），點P的運動時間為t（秒）．
（1）證明矩形PQHC的周長是一個定值．
（2）當矩形PQHC為正方形時，求t的值．
（3）在整個運動過程中，存在全等三角形時，求S的值．
（4）矩形PQHC的對角線PH和CQ的交點為M，作點Q關于直線AB的對稱點N，當MN與△ABC的邊平行或者垂直時，直接寫出此時的t值．發布：2025/6/10 0:30:1組卷：68引用：3難度：0.1