對于平面內三個點P，A，B，給出如下定義：將線段PA與線段PB長度的和叫做線段AB關于點P的折線距離，記為d（P，AB）．例如圖1中，A，B，C三點共線，AB=2，BC=1，則線段AC關于點B的折線距離d（B，AC）=BA+BC=2+1=3，線段AB關于點C的折線距離d（C，AB）=CA+CB=3+1=4．
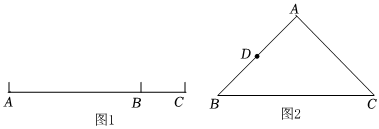
（1）如圖2，△ABC中，AB=AC=22，∠BAC=90°，D是AB中點，
①d（A，DC）=3232．
②P是線段BC上動點，確定點P的位置使得d（P，AD）的值最小，并求出d（P，AD）的最小值．
（2）△ABC中，AB=AC=2，過點C作AC的垂線l,點Q在直線l上，直接寫出d（Q，AB）的最小值的取值范圍．
2
2
2
2
【考點】三角形綜合題．
【答案】3
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/31 14:0:2組卷：148引用：3難度：0.2
相似題
-
1．如圖，已知A（a,b），AB⊥y軸于B，且滿足2a2-2ab+b2-6a+9=0，
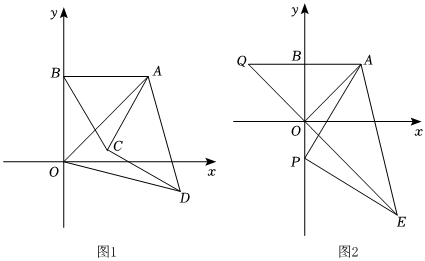
（1）求A點坐標；
（2）分別以AB，AO為邊作等邊三角形△ABC和△AOD，如圖1，試判斷線段AC和DC的數量關系和位置關系，并說明理由；
（3）如圖2，若P為y軸上異于原點O和點B的一個動點，連接PA，過P點作PE⊥PA，且PE=PA，連接AE，射線EO交AB延長線于Q，當P點在y軸上移動時，線段AQ的值是否發生變化．若不變化，求出AQ的值；若變化，請說明理由．發布：2025/6/2 1:30:2組卷：798引用：6難度：0.1 -
2．有共同頂點的△ABC與△ADE中，CA=CB，EA=ED，且∠ACB=∠AED=α，連接BD，CE，線段BD，CE相交于點H．
（1）如圖①，當α=60°時，的值是 ，∠BHC的度數是 ；BDCE
（2）如圖②，當α=90°時，求的值和∠BHC的度數，并說明理由；BDCE
（3）如果α=90°，=2，當點H與△ADE的頂點重合時，請直接寫出ACAE的值．BDDE
發布：2025/6/2 2:0:16組卷：821引用：2難度：0.1 -
3．【證明體驗】
（1）如圖①，在△ABC和△ADE中，∠BAC=∠DAE，AB=AC，AD=AE，連接BD，CE．
求證：BD=CE；
【思考探究】
（2）如圖②，在①的條件下，若AB=4，BC=3，∠ABD=90°，BD=DE，求CE的長；
【拓展延伸】
（3）如圖③，在四邊形ABCD中，AB=AC，BC=4，CD=8，BD=10，∠BAC=2∠ADC，求的值．ABAD
發布：2025/6/2 0:0:1組卷：1312引用：4難度：0.1