如圖，已知A（a,b），AB⊥y軸于B，且滿足2a2-2ab+b2-6a+9=0，
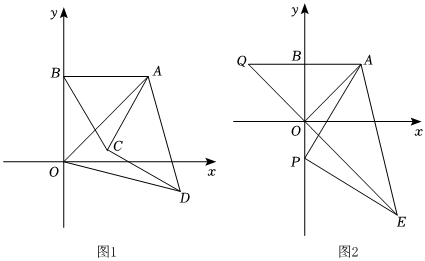
（1）求A點坐標；
（2）分別以AB，AO為邊作等邊三角形△ABC和△AOD，如圖1，試判斷線段AC和DC的數量關系和位置關系，并說明理由；
（3）如圖2，若P為y軸上異于原點O和點B的一個動點，連接PA，過P點作PE⊥PA，且PE=PA，連接AE，射線EO交AB延長線于Q，當P點在y軸上移動時，線段AQ的值是否發生變化．若不變化，求出AQ的值；若變化，請說明理由．
【考點】三角形綜合題．
【答案】（1）A（3，3）；
（2）結論：AC=CD，AC⊥CD．證明見解析部分；
（3）結論：AQ是定值=6．證明見解析部分．
（2）結論：AC=CD，AC⊥CD．證明見解析部分；
（3）結論：AQ是定值=6．證明見解析部分．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/2 1:30:2組卷：798引用：6難度：0.1
相似題
-
1．在平面直角坐標系中，O為原點，點A（3，0），點B（0，4），把△ABO繞點B逆時針旋轉，得△A'BO′．點A，O旋轉后的對應點為A'，O'，記旋轉角為α．
（Ⅰ）如圖①，若α=90°，求AA'的長；
（Ⅱ）如圖②．若α=45°，求點O'的坐標；
（Ⅲ）若M為AB邊上的一動點，在OB上取一點N（0，1），將△ABO繞點B逆時針旋轉一周，求MN的取值范圍（直接寫出結果即可）．發布：2025/6/3 17:0:2組卷：687引用：4難度：0.4 -
2．如圖，在△ABC中，AB=50cm,BC=30cm,AC=40cm.
（1）求證：∠ACB=90°
（2）求AB邊上的高．
（3）點D從點B出發在線段AB上以2cm/s的速度向終點A運動，設點D的運動時間為t（s）．
①BD的長用含t的代數式表示為．
②當△BCD為等腰三角形時，直接寫出t的值．發布：2025/6/3 15:0:1組卷：314引用：2難度：0.3 -
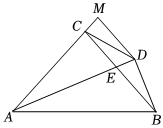3．如圖，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于點E，BD⊥AE于點E，DM⊥AC交AC的延長線于點M，連接CD，下列結論正確的是 ．
①AC+CE=AB；
②為定值；AMAC+AB
③∠CDA=45°；
④．CD=12AE發布：2025/6/3 16:0:1組卷：34引用：1難度：0.3