在正方形ABCD中，AB=6，將正方形ABCD繞點(diǎn)A旋轉(zhuǎn)30°，得到正方形AEFG，則BG的長(zhǎng)為
6或
6
3
6或
6
3
．

【答案】6或

【解答】

【點(diǎn)評(píng)】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

發(fā)布：2025/5/24 1:0:1組卷：92引用：4難度：0.6

相似題

1．如圖，在△ABC中，∠BAC=50°，∠C=25°，將△ABC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)α角度（0°＜α＜180°）得到△ADE．若DE∥AB，則α的值為（　　）
A．65° B．75° C．85° D．95°
發(fā)布：2025/5/24 7:30:1組卷：755引用：13難度：0.7
解析
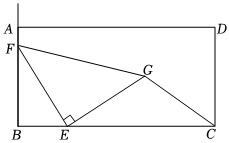2．如圖，在矩形ABCD中，點(diǎn)E為BC上定點(diǎn)，BC=2AB=4BE=8，點(diǎn)F為射線BA上一動(dòng)點(diǎn)，連接EF，將EF繞點(diǎn)E順時(shí)針旋轉(zhuǎn)90°，點(diǎn)F落點(diǎn)為點(diǎn)G，則CG的最小值為
．
發(fā)布：2025/5/24 6:0:2組卷：211引用：1難度：0.6
解析
3．如圖，正方形ABCD和正方形CEFG邊長(zhǎng)分別為a和b,正方形CEFG繞點(diǎn)C旋轉(zhuǎn)，給出下列結(jié)論：①BE=DG；②BE⊥DG；③DE²+BG²=2a²+2b²；④當(dāng)∠DCE=60°時(shí)，S_△DCE=
3
S_△BCE．其中正確的結(jié)論是（　　）
A．①②③ B．②③④ C．①②④ D．①②③④
發(fā)布：2025/5/24 9:0:1組卷：975引用：2難度：0.3
解析

相關(guān)試卷

在正方形ABCD中，AB=6，將正方形ABCD繞點(diǎn)A旋轉(zhuǎn)30°，得到正方形AEFG，則BG的長(zhǎng)為 6或636或63．