數學模型學習與應用：
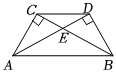
（1）學習：如圖1，∠BAD=90°，AB=AD，BC⊥AC于點C，DE⊥AC于點E．由∠1+∠2=∠2+∠D=90°，得∠1=∠D；又∠ACB=∠AED=90°，可以通過推理得到△ABC≌△DAE，進而得到AC=

DE

DE

，BC=

AE

AE

．我們把這個數學模型稱為“一線三等角”模型．
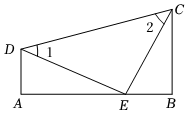
（2）應用：如圖2，在△ABC中，AB=AC，點D，A，E都在直線l上，并且∠BDA=∠AEC=∠BAC=α．若DE=a,BD=b,求CE的長度（用含a,b的代數式表示）；
（3）拓展：如圖3，在（2）的條件下，若α=120°，且△ACF是等邊三角形，試判斷△DEF的形狀，并說明理由．