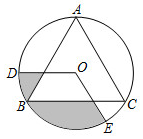
如圖，等邊三角形ABC內(nèi)接于⊙O，點D，E是⊙O上兩點，且∠DOE=120°，若OD=2，則圖中陰影部分的面積為4π3-34π3-3．
4
π
3
-
3
4
π
3
-
3
【答案】
4
π
3
-
3
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/5/22 2:30:1組卷：165引用：3難度：0.5
相似題
-
1．下列說法錯誤的是（ ）
發(fā)布：2025/5/22 9:0:1組卷：397引用：3難度：0.7 -
2．△ABC是⊙O的內(nèi)接三角形，且∠BOC=70°，則∠BAC=．
發(fā)布：2025/5/22 15:0:2組卷：72引用：2難度：0.5 -
3．請閱讀下列材料，并完成相應的任務(wù)：
阿基米德折弦定理
阿基米德（archimedes,公元前287～公元前212年，古希臘）是有史以來最偉大的數(shù)學家之一，他與牛頓、高斯并稱為三大數(shù)學王子．
阿拉伯Al-Birnmi（973～1050年）的譯文中保存了阿基米德折弦定理的內(nèi)容，蘇聯(lián)在1964年根據(jù)Al-Birnmi譯本出版了俄文版《阿基米德全集》，第一題就是阿基米德折弦定理．
阿基米德折弦定理：如圖1，AB和BC是⊙O的兩條弦（即折線ABC是圓的一條折弦），AB＞BC，D是的中點，則從D向AB所作垂線的垂足E是折弦ABC的中點，即AE=EB+BC．?ABC
下面是運用“補短法”證明AE=EB+BC的部分證明過程．
證明：如圖2，延長CB到點F，使得CF=AE，連接DA、DB、DC和DF．
∵D是的中點，?ABC
∴DA=DC．
任務(wù)：
（1）請按照上面的證明思路，寫出該證明的剩余部分；
（2）已知等邊△ABC內(nèi)接于⊙O，AB=6，D為⊙O上一點，∠ABD=45°，AE⊥BD于點E，求△BDC的周長是 ．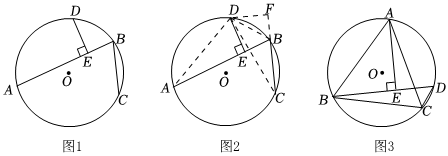
發(fā)布：2025/5/22 15:30:1組卷：579引用：1難度：0.3
相關(guān)試卷