小敏同學有非常良好的學習習慣,在解答人教版數學八(上)教科書P29第8題時,順利完成后并進行了相應探究,請你經歷的思考過程,回答下列問題.
課本真題:如圖1,在△ABC中,AD是高,AE是角平分線,∠B=60°,∠C=70°,求∠DAE的度數.
小敏思路:根據∠C的度數先求出∠CAD,有∠B、∠C的度數在求出∠CAE,則結果可得.
(1)請直接寫出小敏求出的∠DAE=5°5°.
(2)善于思考的小敏想,∠B、∠C與∠DAE會不會存在固定的數量關系?于是,她試了幾組∠B、∠C的度數后(∠C>∠B),猜想出∠B、∠C與∠DAE的關系為 ∠EAD=12(∠C-∠B)∠EAD=12(∠C-∠B),請證明小敏的猜想;(先填空,再證明)
(3)在(2)的基礎上,小敏想到,因為∠DAE與∠AED互余,所以她得出∠B、∠C與∠DAE的關系為2∠AED=180°-(∠C-∠B).而后,小敏在原圖形的基礎上作了AE的垂直平分線,交BC的延長線與F點,連接AF,如圖2,請你仔細思考,直接寫出∠B、∠ACF、∠EAF之間的數量關系 ∠B+∠ACF=2∠EAF∠B+∠ACF=2∠EAF.
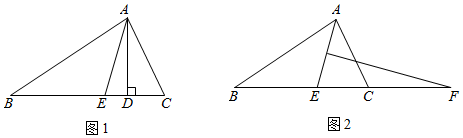
1
2
1
2
【考點】全等三角形的判定與性質;線段垂直平分線的性質.
【答案】5°;∠EAD=(∠C-∠B);∠B+∠ACF=2∠EAF
1
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/8/2 8:0:9組卷:130引用:3難度:0.2





