在平面直角坐標(biāo)系中，△ABC的三個頂點坐標(biāo)分別為A（1，-2），B（2，-1），C（4，-3）．
（1）畫出△ABC關(guān)于x軸對稱的△A1B1C1；
（2）以點O為位似中心，在網(wǎng)格中畫出△A1B1C1的位似圖形△A2B2C2，使△A2B2C2與△A1B1C1的相似比為2：1；
（3）設(shè)點P（a,b）為△ABC內(nèi)一點，則依上述兩次變換后點P在△A2B2C2內(nèi)的對應(yīng)點P2的坐標(biāo)是（2a,-2b）（2a,-2b）．
【答案】（2a，-2b）
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/22 17:30:2組卷：1233引用：28難度：0.7
相似題
-
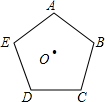1．已知五邊形ABCDE如圖，以點O為位似中心，將五邊形ABCDE作位似變換，使原圖形與它的像的位似比為2：1．
（1）根據(jù)要求作出它的像（不要求寫作法，保留作圖痕跡）；
（2）若五邊形ABCDE的面積為20，求它的像的面積S．發(fā)布：2025/5/29 4:30:1組卷：92引用：2難度：0.1 -
2．在如圖的△ABC外部選擇合適的位似中心O，把△ABC三邊縮小為原來的一半．發(fā)布：2025/5/27 6:30:1組卷：54引用：1難度：0.7 -
3．如圖，方格紙中的每個小正方格都是邊長為1的正方形，我們把以格點間連接為邊的三角形稱為“格點三角形”，圖中的△ABC就是格點三角形，在建立平面直角坐標(biāo)系后，O是坐標(biāo)原點，B、C兩點的坐標(biāo)分別為（3，-1）、（2，1）．
（1）以O(shè)點為位似中心在y軸的左側(cè)將△OBC放大兩倍（即新圖與原圖的相似比為2），在該坐標(biāo)系中畫出圖形；
（2）分別寫出B、C兩點的對應(yīng)點B′、C′的坐標(biāo)；
（3）如果△OBC內(nèi)部一點M的坐標(biāo)為（x,y），寫出M的對應(yīng)點M′的坐標(biāo)．發(fā)布：2025/5/26 10:0:1組卷：113引用：3難度：0.7