2022-2023學年安徽省合肥市琥珀中學教育集團九年級（上）第二次調研數學試卷

一、選擇題（每題4分，共計40分.每題給出四個選項A、B、C、D，其中只有一個符合題目要求.）

• 1．已知在Rt△ABC中，∠C=90°．若sinA=

  2

  2

  ，則sinB等于（　　）

  A． 1 2

  B． 2 2

  C． 3 2

  D．1
  組卷：576引用：20難度：0.9

  解析

• 2．將拋物線y=-2x²+1向右平移1個單位，再向下平移2個單位后所得到的拋物線為（　　）

  A．y=-2（x+1）2-1	B．y=-2（x-1）2+3
  C．y=-2（x-1）2-1	D．y=-2（x+1）2+3
  組卷：313引用：12難度：0.8

  解析

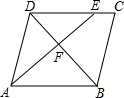• 3．如圖，在平行四邊形ABCD中，點E在邊DC上，DE：EC=3：1，連接AE交BD于點F，則△DEF的面積與△BAF的面積之比為（　　）

  A．3：4

  B．9：16

  C．9：1

  D．3：1
  組卷：15637引用：140難度：0.9

  解析

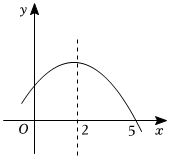• 4．如圖所示的是二次函數y=ax²+bx+c的部分圖象，由圖象可知不等式ax²+bx+c＜0的解集是（　　）

  A．-1＜x＜5

  B．x＞5

  C．x＜-1且x＞5

  D．x＜-1或x＞5
  組卷：2066引用：34難度：0.5

  解析

• 5．如圖，在△ABC中，點D、E分別在邊AB、AC上，則在下列五個條件中：①∠AED=∠B；②DE∥BC；③

  AD

  AC

  =

  AE

  AB

  ；④AD?BC=DE?AC；⑤∠ADE=∠C，能滿足△ADE∽△ACB的條件有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：3587引用：14難度：0.7

  解析

• 6．若正比例函數y=mx（m≠0），y隨x的增大而減小，則它和二次函數y=mx²+m的圖象大致是（　　）

  A．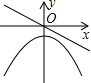

  B．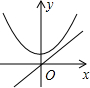

  C．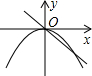

  D．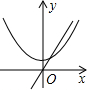
  組卷：2517引用：112難度：0.9

  解析

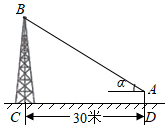• 7．如圖，在離鐵塔BC底部30米的D處，用測角儀從點A處測得塔頂B的仰角為α=30°，測角儀高AD為1.5米，則鐵塔的高BC為（　　）

  A．16.5米	B．（10 3 +1.5）米
  C．（15 3 +1.5）米	D．（15 2 +1.5）米
  組卷：722引用：4難度：0.5

  解析

三、解答題（15，16，17，18，每題8分；19，20每題10分；21，22每題12分，23題14分）

• 22．如圖，AB⊥BC，DC⊥BC，E是BC上一點，使得AE⊥DE；
  （1）求證：△ABE∽△ECD；
  （2）若AB=4，AE=BC=5，求CD的長；
  （3）當△AED∽△ECD時，請寫出線段AD、AB、CD之間數量關系，并說明理由．
  組卷：8683引用：15難度：0.1

  解析

• 23．如圖1為北京冬奧會“雪飛天”滑雪大跳臺賽道的橫截面示意圖．取水平線OE為x軸，鉛垂線OD為y軸，建立平面直角坐標系．運動員以速度v（m/s）從D點滑出，運動軌跡近似拋物線y=-ax²+2x+20（a≠0）．某運動員7次試跳的軌跡如圖2．在著陸坡CE上設置點K（與DO相距32m）作為標準點，著陸點在K點或超過K點視為成績達標．
  
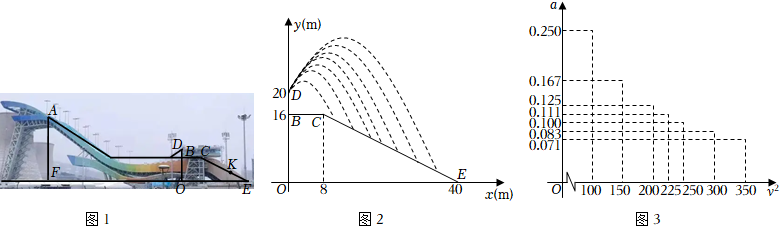
  （1）求線段CE的函數表達式（寫出x的取值范圍）．
  （2）當a=

  1

  9

  時，著陸點為P，求P的橫坐標并判斷成績是否達標．
  （3）在試跳中發現運動軌跡與滑出速度v的大小有關，進一步探究，測算得7組a與v²的對應數據，在平面直角坐標系中描點如圖3．
  ①猜想a關于v²的函數類型，求函數表達式，并任選一對對應值驗證．
  ②當v為多少m/s時，運動員的成績恰能達標（精確到1m/s）？（參考數據：

  3

  ≈1.73，

  5

  ≈2.24）
  組卷：2892引用：11難度：0.4

  解析