如圖，在△ABC和△CDE中，AC=BC，CD=CE，連接AD，BE交于點M．
（1）如圖1，當點B，C，D在同一條直線上，且∠ACB=∠DCE時，可以得到圖中的一對全等三角形，即≌；
（2）當點D不在直線BC上時，如圖2位置，且∠ACB=∠DCE=α．
①試說明AD=BE；
②直接寫出∠EMD的大小（用含α的代數式表示）．
【考點】三角形綜合題．
【答案】（1）△BCE，△ACD；
（2）①見解析；②α．
（2）①見解析；②α．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/27 8:0:10組卷：91引用：3難度：0.5
相似題
-
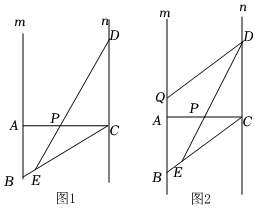1．綜合與實踐：
問題情境：數學活動課上，王老師出示了一個問題：
如圖1，直線m∥n,點A、B在直線m上（點B在點A的下方），過點A作AC⊥n于點C，連接BC，以C為圓心CA為半徑作弧，交直線n于點D，交BC于點E．求證：∠ABC=2∠CDE．
獨立思考：（1）請解答王老師提出的問題．
實踐探究：（2）DE與AC交于點P，在原有問題條件不變的情況下，王老師提出新問題，請你解答．
“猜想出AB、BC、PC的數量關系，并證明．”
問題解決：（3）過點D作DQ∥BC交m于點Q（點Q在點A上方），數學活動小組同學對上述問題進行特殊化研究之后發現，當AQ=BE時，線段BE和AB有一定的數量關系，該小組提出下面的問題，請你解答．
“如圖2，當AQ=BE時，求的值．”DPAB發布：2025/6/14 20:0:1組卷：171引用：2難度：0.1 -
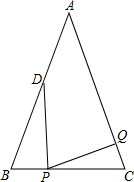2．如圖，已知△ABC中，AB=AC=6cm,∠B=∠C，BC=4cm,點D為AB的中點．
（1）如果點P在線段BC上以1cm/s的速度由點B向點C運動，同時，點Q在線段CA上由點C向點A運動．
①若點Q的運動速度與點P的運動速度相等，經過1秒后，△BPD與△CPQ是否全等，請說明理由．
②若點Q的運動速度與點P的運動速度不相等，當點Q的運動速度為 cm/s時，在某一時刻也能夠使△BPD與△CPQ全等．
（2）若點Q以②中的運動速度從點C出發，點P以原來的運動速度從點B同時出發，都按逆時針方向沿△ABC的三邊運動．求經過多少秒后，點P與點Q第一次相遇，并寫出第一次相遇點在△ABC的哪條邊上？發布：2025/6/14 20:0:1組卷：112引用：2難度：0.3 -
3．在△ABC和△DBE中，CA=CB，EB=ED，點D在AC上．
（1）如圖1，若∠ABC=∠DBE=60°，求證：∠ECB=∠A；
（2）如圖2，設BC與DE交于點F．當∠ABC=∠DBE=45°時，求證：CE∥AB；
（3）在（2）的條件下，若tan∠DEC=時，求12的值．EFDF發布：2025/6/15 3:0:1組卷：1383引用：3難度：0.4