 在初中階段的函數學習中,我們經歷了“確定函數的表達式一一利用函數圖象研究其性質一一運用函數解決問題”的學習過程.在畫函數圖象時,我們通過描點或平移的方法畫出了所學的函數圖象.同時,我們也學習了絕對值的意義|a|=
在初中階段的函數學習中,我們經歷了“確定函數的表達式一一利用函數圖象研究其性質一一運用函數解決問題”的學習過程.在畫函數圖象時,我們通過描點或平移的方法畫出了所學的函數圖象.同時,我們也學習了絕對值的意義|a|=a(a≥0) -a(a<0)
.
結合上面經歷的學習過程,現在來解決下面的問題:
在函數y=|kx-3|+b中,當x=2時,y=-4;當x=0時,y=-1.
(1)求這個函數的表達式;
(2)在給出的平面直角坐標系中,請用你喜歡的方法畫出這個函數的圖象,并寫出這個函數的一條性質;
(3)已知函數y=12x-3的圖象如圖所示,結合你所畫的函數圖象,直接寫出不等式|kx-3|+b≤12x-3的解集.
(4)若方程|x2-6x|-a=0有四個不相等的實數根,則實數a的取值范圍是 0<a<90<a<9.
|
a
|
=
a ( a ≥ 0 ) |
- a ( a < 0 ) |
y
=
1
2
x
-
3
|
kx
-
3
|
+
b
≤
1
2
x
-
3
【答案】0<a<9
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/24 4:30:1組卷:1420引用:4難度:0.2
相似題
-
1.關于x的方程(m-2)x2+2x+1=0有實數根,則偶數m的最大值為.
發布:2025/5/24 9:0:1組卷:884引用:10難度:0.7 -
2.一元二次方程ax2+x-2=0有兩個不相等實數根,則a的取值范圍是( )
A.a <18B.a= -18C.a 且a≠0>-18D.a 且a≠0>18發布:2025/5/24 8:30:1組卷:316引用:11難度:0.7 -
3.閱讀與思考
下面是小宇同學的數學小論文,請仔細閱讀并完成相應的任務.
任務:(1)上面小論文中的分析過程,主要運用的數學思想是 (從下面選項中選出兩個即可);用函數觀點認識一元二次方程根的情況
我們知道,一元二次方程ax2+bx+c=0(a≠0)的根就是相應的二次函數y=ax2+bx+c(a≠0)的圖象(稱為拋物線)與x軸交點的橫坐標.拋物線與x軸的交點有三種情況:有兩個交點、有一個交點、無交點.與此相對應,一元二次方程的根也有三種情況:有兩個不相等的實數根、有兩個相等的實數根、無實數根.因此可用拋物線與x軸的交點個數確定一元二次方程根的情況.
下面根據拋物線的頂點坐標(-,b2a)和一元二次方程根的判別式Δ=b2-4ac,分別分a>0和a<0兩種情況進行分析:4ac-b24a
(1)a>0時,拋物線開口向上.
①當Δ=b2-4ac>0時,有4ac-b2<0.∵a>0,∴頂點縱坐標<0.4ac-b24a
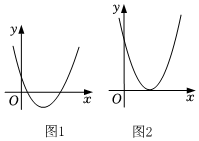
∴頂點在x軸的下方,拋物線與x軸有兩個交點(如圖1).
②當Δ=b2-4ac=0時,有4ac-b2=0.∵a>0,∴頂點縱坐標=0.4ac-b24a
∴頂點在x軸上,拋物線與x軸有一個交點(如圖2).
∴一元二次方程ax2+bx+c=0(a≠0)有兩個相等的實數根.
③當Δ=b2-4ac<0時,
……
(2)a<0時,拋物線開口向下.
……
A.數形結合
B.統計思想
C.分類討論
D.轉化思想
(2)請參照小論文中當a>0時①②的分析過程,寫出③中當a>0,Δ<0時,一元二次方程根的情況的分析過程,并畫出相應的示意圖;
(3)實際上,除一元二次方程外,初中數學還有一些知識也可以用函數觀點來認識.例如:可用函數觀點來認識一元一次方程的解.請你再舉出一例為 .發布:2025/5/24 8:30:1組卷:1290引用:13難度:0.6


