閱讀與思考
下面是小宇同學的數學小論文，請仔細閱讀并完成相應的任務．
| 用函數觀點認識一元二次方程根的情況 我們知道，一元二次方程ax2+bx+c=0（a≠0）的根就是相應的二次函數y=ax2+bx+c（a≠0）的圖象（稱為拋物線）與x軸交點的橫坐標．拋物線與x軸的交點有三種情況：有兩個交點、有一個交點、無交點．與此相對應，一元二次方程的根也有三種情況：有兩個不相等的實數根、有兩個相等的實數根、無實數根．因此可用拋物線與x軸的交點個數確定一元二次方程根的情況． 下面根據拋物線的頂點坐標（- b 2 a 4 ac - b 2 4 a （1）a＞0時，拋物線開口向上． ①當Δ=b2-4ac＞0時，有4ac-b2＜0．∵a＞0，∴頂點縱坐標 4 ac - b 2 4 a ∴頂點在x軸的下方，拋物線與x軸有兩個交點（如圖1）． ②當Δ=b2-4ac=0時，有4ac-b2=0．∵a＞0，∴頂點縱坐標 4 ac - b 2 4 a ∴頂點在x軸上，拋物線與x軸有一個交點（如圖2）． ∴一元二次方程ax2+bx+c=0（a≠0）有兩個相等的實數根． ③當Δ=b2-4ac＜0時， …… （2）a＜0時，拋物線開口向下． ……  |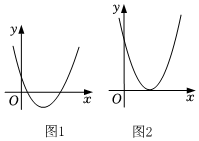
AC
AC
（從下面選項中選出兩個即可）；A．數形結合
B．統計思想
C．分類討論
D．轉化思想
（2）請參照小論文中當a＞0時①②的分析過程，寫出③中當a＞0，Δ＜0時，一元二次方程根的情況的分析過程，并畫出相應的示意圖；
（3）實際上，除一元二次方程外，初中數學還有一些知識也可以用函數觀點來認識．例如：可用函數觀點來認識一元一次方程的解．請你再舉出一例為
可用函數觀點認識二元一次方程組的解（答案不唯一）
可用函數觀點認識二元一次方程組的解（答案不唯一）
．【考點】根的判別式．
【答案】AC；可用函數觀點認識二元一次方程組的解（答案不唯一）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：1287引用：13難度：0.6
相似題
-
1．對于一元二次方程ax2+bx+c=0（a≠0），下列說法：
①若a+c=b,則b2-4ac≥0；
②若方程ax2+c=0有兩個不相等的實根，則方程ax2+bx+c=0必有兩個不相等的實根；
③若x=c是方程ax2+bx+c=0的一個根，則一定有ac+b+1=0成立；
④若x=x0是一元二次方程ax2+bx+c=0的根，則；b2-4ac=（2ax0+b）2
其中正確的（ ）發布：2024/12/23 13:0:2組卷：504引用：6難度：0.5 -
2．已知關于x的一元二次方程mx2-3（m+1）x+2m+3=0
（1）如果該方程有兩個不相等的實數根，求m的取值范圍；
（2）在（1）的條件下，當該方程的兩個根都是整數，求正整數m的值．發布：2024/12/23 11:0:1組卷：988引用：4難度：0.6 -
3．已知關于x的一元二次方程x2-（2k+1）x+k2+k=0．
（1）求證：方程有兩個不相等的實數根；
（2）若△ABC的兩邊AB，AC的長是這個方程的兩個實數根，第三邊BC的長為5，當△ABC是直角三角形時，求k的值．發布：2024/12/23 18:0:1組卷：3012引用：13難度：0.7