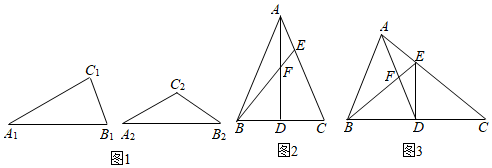
如圖1，在△A1B1C1和△A2B2C2中，A1B1=A2B2，∠A1=∠A2，∠B1=2∠B2，我們把△A1B1C1和△A2B2C2稱為“等邊倍角”三角形，其中A1B1和A2B2為對應(yīng)等邊．
△ABC中，D，E分別是BC，AC邊上的點(diǎn)（不與端點(diǎn)重合），AD與BE相交于點(diǎn)F．
（1）如圖2，若AB=AC≠BC．
①當(dāng)AD⊥BC時(shí)，圖中能與△ABC構(gòu)成“等邊倍角”三角形的是△ABD、△ACD△ABD、△ACD；（直接寫出，不必證明）
②當(dāng)AD與BC不垂直時(shí)，若△ABE與△ADC是“等邊倍角”三角形，其中AB和AC為對應(yīng)等邊，求∠AFE的度數(shù)．
（2）如圖3，連接DE，若DE平分∠BEC，BE=2AE，點(diǎn)F是AD的中點(diǎn)，求證：△ABF和△ADE是“等邊倍角”三角形．
【考點(diǎn)】全等三角形的判定與性質(zhì)；角的計(jì)算．
【答案】△ABD、△ACD
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/20 16:30:1組卷：1687引用：5難度：0.4
相似題
-
1．如圖，已知AP∥BC，∠PAB的平分線與∠CBA的平分線相交于點(diǎn)E，CE的連線交AP于點(diǎn)D，求證：AD+BC=AB．發(fā)布：2025/6/20 22:30:2組卷：9771引用：7難度：0.4 -
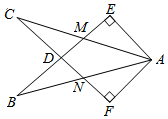2．如圖，在Rt△AEB和Rt△AFC中，∠E=∠F=90°，BE=CF，BE與AC相交于點(diǎn)M，與CF相交于點(diǎn)D，AB與CF相交于點(diǎn)N，∠EAC=∠FAB．有下列結(jié)論：①∠B=∠C；②CD=DN；③CM=BN；④△ACN≌△ABM．其中正確結(jié)論的個(gè)數(shù)是（ ）發(fā)布：2025/6/20 22:30:2組卷：2953引用：15難度：0.4 -
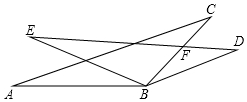3．如圖，BA=BE，∠A=∠E，∠ABE=∠CBD，ED交BC于點(diǎn)F，且∠FBD=∠D．求證：AC∥BD．
證明：∵∠ABE=∠CBD（已知），
∴∠ABE+∠EBC=∠CBD+∠EBC（ ），
即∠ABC=∠EBD，
在△ABC和△EBD中，，∠ABC=∠EBD（??）=（??）∠A=∠E
∴△ABC≌△EBD（ ），
∴∠C=∠D（ ）．
∵∠FBD=∠D，
∴∠C=（ ），
∴AC∥BD（ ）．發(fā)布：2025/6/20 22:0:2組卷：772引用：3難度：0.9