綜合與實踐
【問題情境】
在數學綜合與實踐課上，老師讓同學們借助“兩條平行線AB，CD和一副直角三角尺”開展數學活動．
【操作發現】
（1）如圖1，小明把三角尺60°角的頂點G放在直線CD上，∠F=90°，若∠1=2∠2，則∠1=8080°．
（2）如圖2，小穎把等腰直角三角尺的兩個銳角的頂點E，G分別放在直線AB，CD上，請用等式表示∠AEF與∠FGC之間滿足的數量關系 ∠AEF+∠FGC=90°∠AEF+∠FGC=90°.（不用證明）
【綜合應用】
（3）在圖2的基礎上，小亮把三角尺60°角的頂點放在點F處，即∠PFQ=60°，如圖3，FM平分∠EFP交直線AB于點M，FN平分∠QFG交直線CD于點N．將含60°角的三角尺繞著點F轉動，且使FG始終在∠PFQ的內部，請問∠AMF+∠CNF的值是否發生變化？若不變，求出它的值；若變化，說明理由．
?
【考點】平行線的性質．
【答案】80；∠AEF+∠FGC=90°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/29 8:0:10組卷：134引用：1難度：0.6
相似題
-
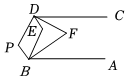1．如圖，已知AB∥CD，∠ABP和∠CDP的平分線相交于點E，∠ABE和∠CDE的平分線相交于點F．
（1）若∠CDF=21°，∠ABF=33°，求∠DPB的度數；
（2）若∠BFD=54°，求∠BPD和∠BED的度數．發布：2025/6/15 3:30:1組卷：222引用：1難度：0.4 -
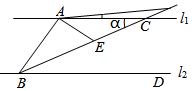2．如圖，AC∥BD，BC平分∠ABD，設∠ACB為α，點E是射線BC上的一個動點．
（1）若α=30°時，且∠BAE=∠CAE，求∠CAE的度數；
（2）若點E運動到l1上方，且滿足∠BAE=100°，∠BAE：∠CAE=5：1，求a的值；
（3）若∠BAE：∠CAE=n（n＞1），求∠CAE的度數（用含n和α的代數式表示）．發布：2025/6/15 3:30:1組卷：1510引用：8難度：0.6 -
3．已知：兩直線l1，l2滿足l1∥l2，點C，點D在直線l1上，點A，點B在直線l2上，點P是平面內一動點，連接CP，BP，
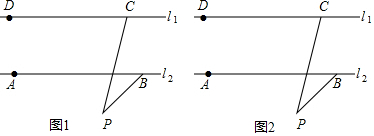
（1）如圖1，若點P在l1、l2外部，則∠DCP、∠CPB、∠ABP之間滿足什么數量關系？請你證明的這個結論；
（2）如圖2，若點P在l1、l2外部，連AC，則∠CAB、∠ACP、∠CPB、∠ABP之間滿足什么數量關系？請你證明的這個結論；（不能用三角形內角和為180°）
（3）若點P在l1、l2內部，且在AC的右側，則∠ACP、∠ABP、∠CAB、∠CPB之間滿足什么數量關系？（不需證明）發布：2025/6/15 4:30:1組卷：1053引用：4難度：0.6