如圖，AB是⊙O的直徑，CD是⊙O的一條弦，CD⊥AB，直線CE為⊙O的切線，CE交AB的延長線于點E，連接DB、BC、CA．
（1）求證：∠BDC=∠BCE；
（2）連接DO，延長DO交AC于點F，延長DB交CE于點G．當F為AC的中點時，求證：DG⊥CE；
（3）若⊙O的半徑為6，在（2）的條件下，求圖中陰影部分面積．
【答案】（1）（2）見解答；
（3）6π-9．
（3）6π-9
3
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/28 8:0:9組卷：371引用：7難度：0.5
相似題
-
1．如圖，AB是⊙O的直徑，點C在⊙O上，過點C的切線交BA的延長線于點D，連接BC．若∠B=α，則∠D的大小為（ ）發(fā)布：2025/5/26 0:0:1組卷：223引用：1難度：0.7 -
2．閱讀資料：我們把頂點在圓上，一邊和圓相交，另一邊和圓相切的角叫做弦切角，如圖1中∠CBD即為弦切角．同學(xué)們研究發(fā)現(xiàn)：A為圓上任意一點，當弦AB經(jīng)過圓心O，且DB切⊙O于點B時，易證：弦切角∠CBD=∠A．
問題拓展：如圖2，點A是優(yōu)弧BC上任意一點，DB切⊙O于點B，求證：∠CBD=∠A．
證明：連接BO并延長交⊙O于點A′，連接A′C，如圖2所示．
∵DB與⊙O相切于點B，
∴∠A′BD=．
∴∠A′BC+∠CBD=90°．
∵A′B′是直徑，
∴∠A′CB=90° （ ）．
∴∠A′+∠A′BC=90°．
∴∠CBD=∠A′（ ）．
又∵∠A′=∠A（ ），
∴∠CBD=∠A．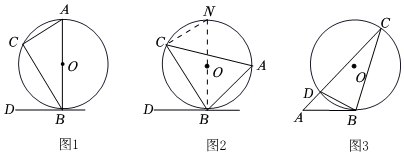
（1）將上述證明過程及依據(jù)補充完整；
（2）如圖3，△ABC的頂點C在⊙O上，AC和⊙O相交于點D，且AB是⊙O的切線，切點為B，連接BD．若AD=2，CD=6，BD=3，求BC的長．發(fā)布：2025/5/26 0:30:1組卷：252引用：1難度：0.6 -
3．如圖，△ABC內(nèi)接于⊙O，AC為⊙O直徑，過點B的切線交CA的延長線于點P．若∠P=32°，則∠ACB的度數(shù)是（ ）發(fā)布：2025/5/26 0:30:1組卷：223引用：1難度：0.6
相關(guān)試卷