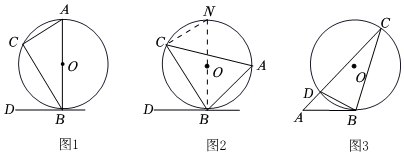
閱讀資料：我們把頂點在圓上，一邊和圓相交，另一邊和圓相切的角叫做弦切角，如圖1中∠CBD即為弦切角．同學們研究發現：A為圓上任意一點，當弦AB經過圓心O，且DB切⊙O于點B時，易證：弦切角∠CBD=∠A．
問題拓展：如圖2，點A是優弧BC上任意一點，DB切⊙O于點B，求證：∠CBD=∠A．
證明：連接BO并延長交⊙O于點A′，連接A′C，如圖2所示．
∵DB與⊙O相切于點B，
∴∠A′BD=90°90°．
∴∠A′BC+∠CBD=90°．
∵A′B′是直徑，
∴∠A′CB=90° （ 直徑所對的圓周角是直角直徑所對的圓周角是直角）．
∴∠A′+∠A′BC=90°．
∴∠CBD=∠A′（ 同角的余角相等同角的余角相等）．
又∵∠A′=∠A（ 同弧所對的圓周角相等同弧所對的圓周角相等），
∴∠CBD=∠A．
（1）將上述證明過程及依據補充完整；
（2）如圖3，△ABC的頂點C在⊙O上，AC和⊙O相交于點D，且AB是⊙O的切線，切點為B，連接BD．若AD=2，CD=6，BD=3，求BC的長．
【答案】90°；直徑所對的圓周角是直角；同角的余角相等；同弧所對的圓周角相等
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/26 0:30:1組卷：252引用：1難度：0.6
相似題
-
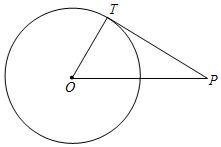1．如圖，已知⊙O的半徑為1，點P是⊙O外一點，且OP=2．若PT是⊙O的切線，T為切點，連結OT，則PT=．發布：2025/5/26 7:30:2組卷：1504引用：10難度：0.7 -
2．如圖，在△ABC中，BA，BC分別為⊙O的切線，點E和點C為切線點，線段AC經過圓心O且與⊙O相交于D、C兩點，若tanA=，AD=2，則BO的長為．34發布：2025/5/26 7:0:2組卷：43引用：6難度：0.4 -
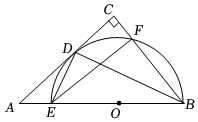3．在Rt△ABC中，∠C=90°，O是斜邊AB上的點，以O為圓心，OB為半徑的
圓與AC相切，切點為D，圓O與邊AB，BC相交于點E，F．
（1）求證：BD平分∠ABC；
（2）連結EF，DE，若tan∠DBF=，AB=10，求半徑的長．55發布：2025/5/26 7:30:2組卷：451引用：1難度：0.6